Chapitre 0: Rappels
Nous allons revoir quelques définitions importantes de première en s’appuyant sur les algorithmes classiques de recherche et de tris.
1 Algorithme naïf de recherche: la recherche en table
Pour rechercher un élément dans une table on pourrait simplement parcourir tout simplement le tableau jusqu’à rencontrer la valeur recherché. C’est ce que l’on appelle la recherche en table.
def recherche(liste, élément):
"""Recherche d'un élément dans une liste
Arguments
---------
liste: liste d'entiers
élément: entier
l'élément cherché
Returns
-------
int: l'indice de l'élément si trouvé ou -1 sinon
"""
for i in range(len(liste)):
if liste[i] == élément:
# l'élément est trouve
return i
# non trouvé
return -1
# Quelques tests
assert recherche([1], 1) == 0
assert recherche([1,6,5], 5) == 2
assert recherche([1,6,5], 7) == -1Même si cet algorithme simple semble faire le travail, il n’est en pratique pas du tout utiliser, car il n’est pas du tout efficace.
Pour mesurer l’efficacité d’un algorithme, on utilise la notion de complexité.
2 Notion de complexité
Si je donne à mon programme une entrée de taille . Quel est l’ordre de grandeur, en fonction de , du nombre d’opérations qu’il va effectuer ?
- Complexité
-
La complexité d’un algorithme est le nombre d’opérations élémentaires(opération arithmétique, comparaison, affectation…)_ effectuées pour obtenir un résultat.
Si on prend l’exemple de l’algorithme précédent, on se rend compte que cela dépend des cas. Expliquez…
Pour pouvoir faire des comparaisons entre algorithmes, l’informaticien étudie souvent la complexité dans le pire des cas.
- Notation asymptotique: grand O
-
On utilise la notation asymptotique () pour décrire le temps d’exécution des algorithmes. On se placera dans le pire des cas(Ex: élément non trouvé pour une recherche) la complexité est alors notée .
Par ordre de complexité croissante:
- complexité logarithmique:
- complexité linéaire:
- complexité quadratique:
- complexité exponentielle:
Dès l’algorithme devient quasiment inutilisable en pratique.
3 Un algorithme efficace: la recherche dichotomique
Quand on cherche un mot dans le dictionnaire, on ne va pas le chercher en les lisant un par un, on va utiliser la méthode de recherche dichotomique vue en première.
Cette méthode est possible dans le cas ou les données ont été au préalable trié, ce pour quoi il existe également des algorithmes efficaces.
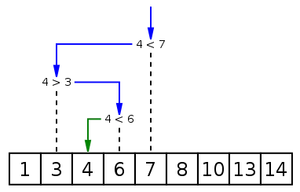
Voici un exemple d’implémentation en Python:
def recherche_dichotomique(liste, élément):
"""Recherche dichotomique
Arguments
---------
liste: liste d'entiers
ATTENTION: la liste doit être triée
élément: entier
l'élément cherché
Returns
-------
int: l'indice de l'élément si trouvé ou -1 sinon
"""
# on initialise les indices début et fin aux extrémités de la liste
début = 0
fin = len(liste)
while début <= fin:
# On se place au milieu de la liste
milieu = (début + fin) // 2 # il, s'agit d'une division entière
if liste[milieu] == élément:
# l'élément est trouvé
return milieu
elif liste[milieu] < élément:
# l'élément est situé dans la sous-liste de droite
début = milieu + 1
else:
# l'élément est situé dans la sous-liste de gauche
fin = milieu - 1
return -1Cet algorithme est beaucoup plus efficace, sa complexité (asymptotique dans le pire des cas) est .
Ceci fait une énorme différence notamment lorsque la taille des données augmente:
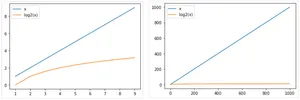
4 Correction d’un algorithme
Pour rappel, un algorithme est une suite d’instructions permettant d’obtenir un résultat.
La correction d’un algorithme est une démonstration qui prouve que l’algorithme permet bien d’obtenir le résultat souhaité.
Nous allons utiliser une méthode répandue semblable au raisonnement par récurrence fondée sur la recherche d’un invariant de boucle.
Pour prouver la correction nous devons montrer les trois points suivants:
- Initialisation: L’invariant est vrai avant la première itération.
- Conservation: si l’invariant est vrai avant une itération, il restera vrai après l’itération.
- Terminaison: la boucle se termine et nous donne le résultat attendu.
Nous allons appliquer cette méthode aux algorithmes de tris vus en première.
5 Correction du tri par sélection
On rappelle le principe de l’algorithme.
Sur un tableau de N éléments (numérotés de 0 à ), le principe du tri par sélection est le suivant : - rechercher le plus petit élément du tableau, et l’échanger avec l’élément d’indice 0 ; - rechercher le second plus petit élément du tableau, et l’échanger avec l’élément d’indice 1 ; - continuer de cette façon jusqu’à ce que le tableau soit entièrement trié.
5.1 Implémentation en Python
En voici une implémentation en python.
def tri_selection(t):
N = len(t)
# Parcourir le tableau jusqu'à l'avant dernière valeur
# en effet la dernière valeur sera forcément la plus grande
for i in range(N-1):
# on recherche l'indice du plus petit élément du sous-tableau de droite
i_min = i
# Parcourir le reste du tableau pour rechercher l'élément le plus petit restant
for j in range(i+1, N):
if t[j] < t[i_min]:
i_min = j
if i_min != i:
# échanger t[i] et t[i_min]
t[i], t[i_min] = t[i_min], t[i]
return tVoici les états successifs du tableau après chaque tour de boucle avec en entrée
[12, 15, 1, 3, 7]:
[1, 15, 12, 3, 7]
[1, 3, 12, 15, 7]
[1, 3, 7, 15, 12]
[1, 3, 7, 12, 15]5.2 Correction de l’algorithme
L’invariant de boucle consiste à montrer que si les premiers éléments du tableau sont triés avant l’itération, alors les premiers éléments seront triés après une itération.
- Initialisation: Au départ, , le sous-tableau trié de gauche ne contient aucun élément
[]. Il est donc forcément trié. - Conservation: Lorsqu’on considère le tour de boucle , le tableau est déjà trié pour les indices à . Grâce à la boucle interne, on trouve le plus petit élément parmi les éléments d’indice à (tous plus grands que l’élément d’indice ), et on le place à l’indice . Après le tour de boucle, le tableau sera donc trié pour les indices de à .
- Terminaison: la boucle se termine lorsqu’on arrive à l’avant-dernier élément du tableau. Le tableau est trié pour les éléments d’indice à , et le dernier élément d’indice est forcément plus grand que l’élément d’indice $ . Le tableau est donc entièrement trié.