Chapitre 2: Algorithmes sur les graphes

import networkx as nx
import matplotlib.pyplot as plt # pour les représentations graphiques

def create_graph():
    G = nx.Graph()

    # Ajout des noeuds nommés
    G.add_node("Paris")
    G.add_node("Lyon")
    G.add_node("Marseille")
    G.add_node("Nice")
    G.add_node("Montpellier")
    G.add_node("Toulouse")
    G.add_node("Rennes")
    G.add_node("Nancy")

    # Ajout des arêtes
    G.add_edge("Paris", "Lyon")
    G.add_edge("Lyon", "Marseille")
    G.add_edge("Nice", "Marseille")
    G.add_edge("Nice", "Lyon")
    G.add_edge("Montpellier", "Marseille")
    G.add_edge("Montpellier", "Toulouse")
    G.add_edge("Paris", "Toulouse")
    G.add_edge("Rennes", "Toulouse")
    G.add_edge("Rennes", "Paris")
    G.add_edge("Nancy", "Paris")
    G.add_edge("Nancy", "Lyon")
    
    return G
# création du graph
G =create_graph()
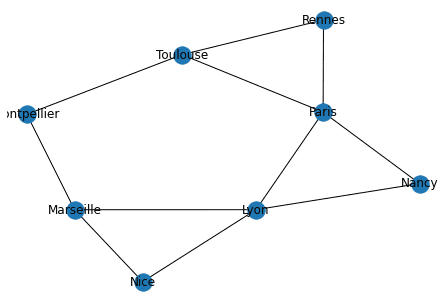
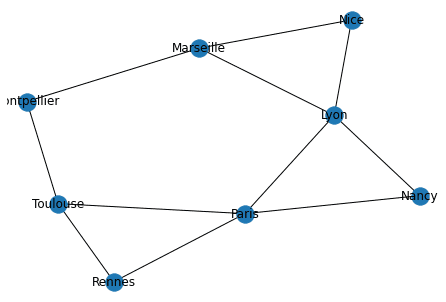
# Représenation graphique
nx.draw(G, with_labels=True) # Il s'agit du graphe et non d'une carte!

nx.to_numpy_matrix(G)

nx.to_dict_of_lists(G)

G = create_graph()
dg =nx.to_dict_of_lists(G)
print("Liste d'adjacence")
print("-----------------")
print(dg)
def parcours_profondeur(G, s):
    # on récupère la liste des voisins
    voisins = G[s]
    # afficher le sommet
    print(s)
    # marquer le sommet s(je le supprime car visité)
    # ATTENTION modification globale car passage par référence
    del G[s]
    # POUR TOUT sommet t voisin du sommet s
    for t in voisins:
        # SI t n'est pas marqué ALORS
        if t in G:
            parcours_profondeur(G, t)


print("\nListe des noeuds visités par notre algorithme")
print("---------------------------------------------")
print(parcours_profondeur(dg, "Nice"))

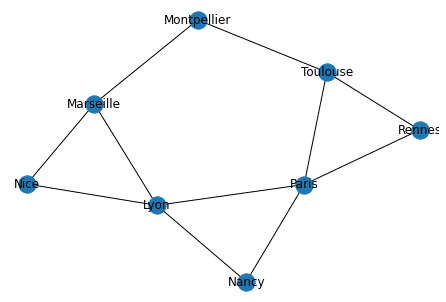
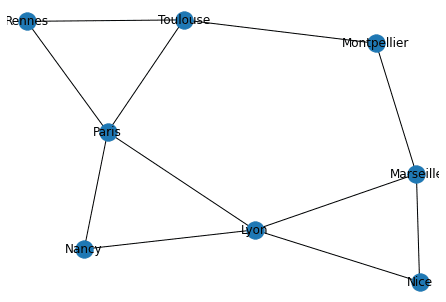
print("\nPour rappel: Forme du graphe")
print("------------------------------")
nx.draw(G, with_labels=True, pos=nx.spring_layout(G))

print("Liste des chemins suivis")
print("------------------------")
print(list(nx.dfs_edges(G, source="Nice")))

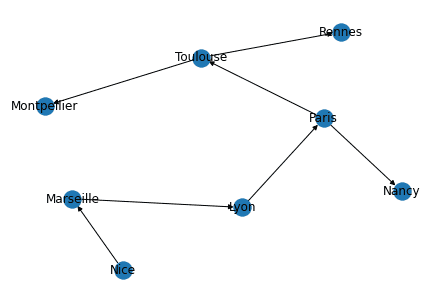
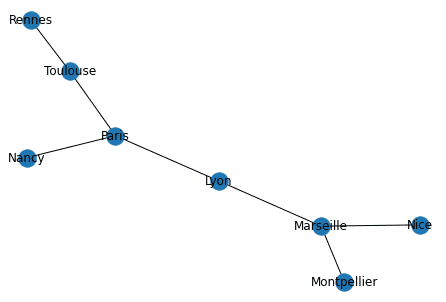
print("\nReprésentation sous forme d'arbre")
print("---------------------------------")
tree = nx.dfs_tree(G, source="Nice")
nx.draw(tree, with_labels=True, pos=nx.spring_layout(G))

# On importe deque pour la file
from collections import deque as file

# On repart d'un graphe tout neuf
G = create_graph()
dg =nx.to_dict_of_lists(G)
print("Liste d'adjacence")
print("-----------------")
print(dg)

# FONCTION parcours_largeur(Graphe G, Sommet s):
def parcours_largeur(G, s):
    #f = CreerFile();
    f = file()
    #f.enfiler(s);
    f.appendleft(s)
    # marquer(s);
    marqués = [s]
    #TANT QUE la file est non vide
    while f:
        #s = f.defiler();
        s = f.pop()
        # afficher(s);
        print(s)
        #POUR TOUT voisin t de s dans G
        for t in G[s]:
            # SI t non marqué
            if t not in marqués:
                #f.enfiler(t);
                f.appendleft(t)
                #marquer(t);
                # marquer le sommet s
                marqués.append(t)
                #node["visited"] =  True
                

print("Liste des noeuds visités par notre algorithme")
print("---------------------------------------------")
print(parcours_largeur(dg, "Nice"))
# je ne sais pas d'ou vient ce dernier None!

print("\nPour rappel: Forme du graphe")
print("------------------------------")
nx.draw(G, with_labels=True, pos=nx.spring_layout(G))

print("Liste des chemins suivis")
print("------------------------")
print(list(nx.bfs_edges(G, source="Nice")))

print("\nReprésentation sous forme d'arbre")
print("---------------------------------")
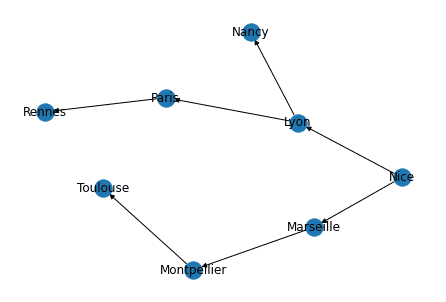
tree = nx.bfs_tree(G, source="Nice")
nx.draw(tree, with_labels=True, pos=nx.spring_layout(G))

# On repart d'un graphe tout neuf
G = create_graph()
# Transformation en liste d'adjacence
dg = nx.to_dict_of_lists(G)

def recherche_cycle(G, s, vus=None):
    # ATTENTION: Liste vide par défaut
    # voir: https://www.lyceum.fr/blog/2021-04-02-comment-passer-une-liste-vide-par-defaut-a-une-fonction-en-python/
    if vus is None:
        vus = []
    # on récupère la liste des voisins
    voisins = G[s]
    # marquer le sommet s
    vus.append(s)
    # POUR TOUT sommet t voisin du sommet s
    for t in voisins:
        if t in vus:
            return True
        # SI t n'est pas marqué ALORS
        else:
            recherche_cycle(G, t, vus)
    return False

print("Présence d'un cycle")
print("-------------------")
print(recherche_cycle(dg, "Nice"))

# Test de la fonction à partir de tous les noeuds de départ
for node in G.nodes:
    # networkx est capable de trouver des cycles
    assert nx.find_cycle(G, source=node)
    # on teste notre fonction maintenant
    assert node, recherche_cycle(dg, node)
    
print("\nPour rappel: Forme du graphe")
print(  "----------------------------")
nx.draw(G, with_labels=True, pos=nx.spring_layout(G))

# Nous supprimons quelques arêtes pour
# retirer les cycles et tester la fonction
def create_acyclic_graph():
    G = create_graph()
    G.remove_edge("Nice", "Lyon")
    G.remove_edge("Nancy", "Lyon")
    G.remove_edge("Paris", "Rennes")
    G.remove_edge("Toulouse", "Montpellier")
    return G

G = create_acyclic_graph()
# Transformation en liste d'adjacence
dg = nx.to_dict_of_lists(G)

print("Présence d'un cycle")
print("-------------------")

print(recherche_cycle(dg, "Paris"))

# Test de la fonction à partir de tous les noeuds de départ
for node in G.nodes:
    try:
        nx.find_cycle(G, source=node)
        assert False
    except nx.NetworkXNoCycle:
        pass
    G = create_acyclic_graph()
    assert not recherche_cycle(dg, node)

print("\nPour rappel: Forme du graphe")
print(  "----------------------------")
nx.draw(G, with_labels=True, pos=nx.spring_layout(G))

# On repart d'un graphe tout neuf
G = create_graph()
# On crée la liste d'adjacence
dg =nx.to_dict_of_lists(G)

# FONCTION plus court chemin(Graphe G, Sommet s, Destination d):
def plus_court_chemin(G, s, d):
    # dictionnaire des prédecesseurs
    prédecesseurs = {s: None}
    # f = CreerFile();
    f = file()
    # f.enfiler(s);
    f.appendleft(s)
    # marquer(s);
    marqués = [s]
    # TANT QUE la file est non vide
    while f:
        # On récupère le noeud
        s = f.pop()
        # POUR TOUT voisin t de s dans G
        for t in G[s]:
            if t == d:
                # Destination trouvée, on remonte le chemin
                ville = s
                chemin = [d]
                while ville:
                    chemin.append(ville)
                    ville = prédecesseurs[ville]
                # On remet dans l'ordre
                chemin.reverse()
                return chemin
            # SI t non marqué
            elif t not in marqués:
                # f.enfiler(t);
                f.appendleft(t)
                # marquer(t);
                marqués.append(t)
                # màJ du dictionnaire de prédecesseurs  
                prédecesseurs[t] = s
    # Destination non trouvée        
    return []
                

print("On teste sur tous les trajets possibles")
print("---------------------------------------")
villes = G.nodes
from itertools import combinations
for source, dest in combinations(villes, 2):
    chemin = plus_court_chemin(dg, source, dest)
    print(f"{source} -> {dest}: {chemin}")

print("\nSi la destination n'est pas trouvée")
print("-----------------------------------")
source, dest = "Nice", "Tokyo"
chemin = plus_court_chemin(dg, source, dest)
print(f"{source} -> {dest}: {chemin}")


print("\nPour vérification: Forme du graphe")
print("------------------------------------")
nx.draw(G, with_labels=True, pos=nx.spring_layout(G))