Chapitre 9: Les oscillateurs énergie et temps
Plan
Énergie cinétique
Il s'agit de l'énergie liée à la vitesse du système.
Remarque: L'énergie cinétique est supérieure ou égale à zéro.
Conversions de vitesses :
- 1 m/s = 3,6 km/h
un véhicule de 1,5 t roule à 50 km/h.
Calculer son énergie cinétique.
Travail d'une force
En physique, le travail noté W est une grandeur algébrique qui permet de mesurer l'énergie transférée par un force à un système.
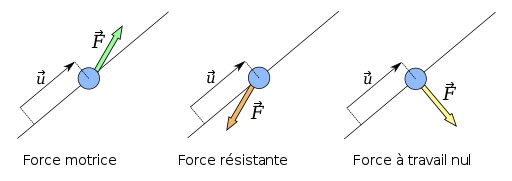
Si au cours du mouvement, la force a pour effet :
- d'augmenter l'énergie du système : W > 0, le travail est moteur.
- De diminuer l'énergie du système : W < 0, le travail est résistant.
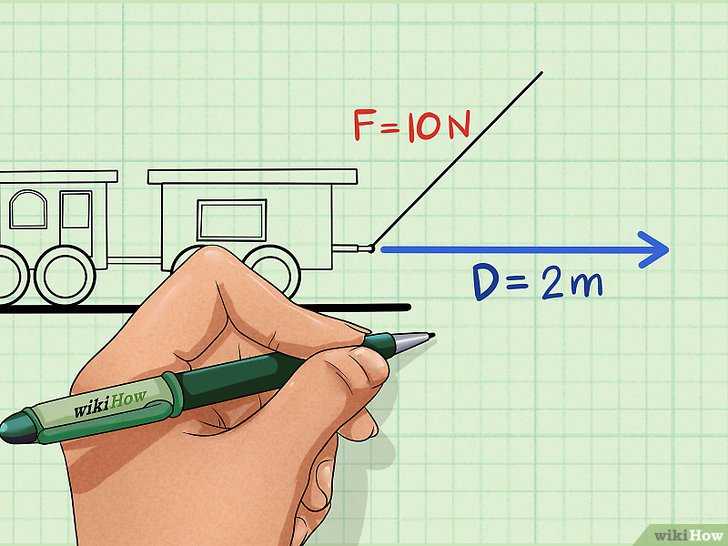
Expression du travail d'une force constante
Le travail d'une force constante lors d'un déplacement d'un point A vers un point B est indépendant du chemin suivi, il a pour expression:
Propriété
Le travail d'une force constante ne dépend pas du chemin suivi lors du déplacement.
Cas particuliers
Si la force est colinéaire au déplacement
Si la force n'est pas colinéaire au déplacement
Travail de forces usuelles
Travail du poids
Le poids est une force constante verticale vers le bas de valeur .
Son travail ne dépend que de la différence de hauteur entre les points de départ et d'arrivée.
By Ilevanat - Own work, CC BY-SA 3.0, Link
Vitesse lors d'une chute
En l'absence de frottements, de quelle hauteur doit tomber un objet pour atteindre une vitesse de 50 km/h ?
Travail d'une force électrostatique
Rappels sur le condensateur
Un condensateur plan est formé de deux plaques métalliques planes séparées par un matériau isolant(le diélectrique).
Lorsque l'on applique une tension aux bornes du condensateur, un champ électrostatique est créé entre les plaques.
Le champ électrostatique est:
- perpendiculaire aux plaques,
- dirigé de la borne + vers la borne -,
- de valeur

By Papa November -
self-made SVG version of Image:Dielectric.png, incorporating Image:Capacitor schematic.svg as its base., CC BY-SA 3.0, Link
Expression du travail de la force électrostatique
La force électrostatique a pour expression:
https://phet.colorado.edu/sims/html/charges-and-fields/latest/charges-and-fields_fr.html
En calculant le travail de la force électrique lors du déplacement d'une charge q d'un point la borne positive vers un point de la borne négative, on obtient:
Expérience de Thomson
Thomson accélérait les électrons avec des condensateurs soumis à une tension de 1 kV. Quelle vitesse avaient les électrons à la sortie du condensateur ?
Travail des forces de frottements
Les forces de frottement dépendent du chemin suivi, on les appelle des forces non conservatives.
Une force de frottement est généralement de sens opposé au déplacement, son travail est alors résistant.
Force de freinage
Calculer la valeur de la force de freinage d'un véhicule de 1,5 t sachant que la distance de freinage à 50 km/h est de 9 m sur sol sec.
Forces conservatives et énergies potentielles
- Force conservative
Une force est dite conservative, si son travail ne dépend pas du chemin suivi.
On peut dans le cas des forces conservatives, associer à une force une énergie potentielle Ep, ou énergie de position.
Par définition, la variation d'énergie potentielle est égale à l'opposé du travail de la force conservative lors du mouvement.
Comme l'énergie potentielle est définie par une variation, l'énergie potentielle d'une force est définie à une constante près.
Conservation de l'énergie mécanique
L'intéret de cette définition est d'assurer la conservation de l'énergie mécanique . Le travail des forces fait augmenter ou diminuer l'énergie cinétique suivant s'il est moteur ou résistant(Il s'agit du théorème de l'énergie cinétique).
D'après la définition de l'énergie potentielle:
On obtient:
La variation d'énergie mécanique du système soumis à une force conservative est nulle, ce qui revient à dire que l'énergie mécanqiue est constante.
Énergie potentielle de pesanteur
C'est l'énergie potentielle associée au travail au poids:
Notations
- : énergie potentielle de pesanteur du système en joule()
- : masse du système étudié en kilogramme()
- : intensité de la pesanteur en mètre par seconde au carré(
- : altitude du système par rapport à l'altitude de référence en mètre()
Énergie potentielle électrique
C'est l'énergie potentielle associée au travail de la force électrique:
Notations
- : énergie potentielle électrique du système en joule()
- : charge électrique du système étudié en Coulomb()
- : potentiel électrique auquel est soumis le système en volt()
Energie mécanique
L'énergie mécanique est la somme de l'énergie cinétique et des énergies potentielles des forces conservatives qui agissent sur le système.
Conservation de l'énergie mécanique
L'énergie mécanique d'un système se conserve si:
- le système n'est soumis qu'à des forces conservatives
- et/ou à des forces non conservatives dont le travail est nul.
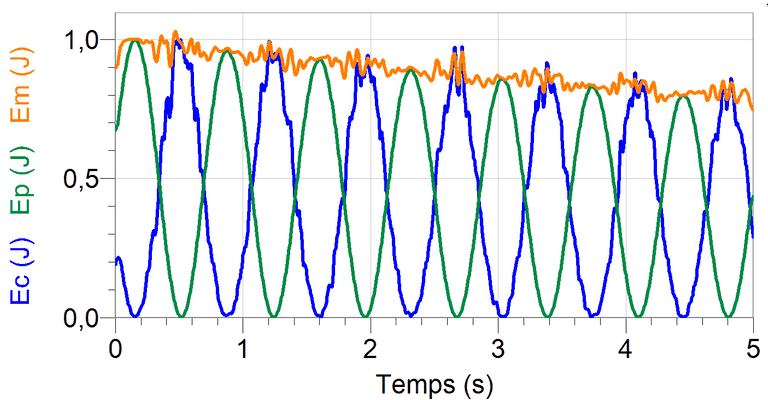
Pendule non amorti
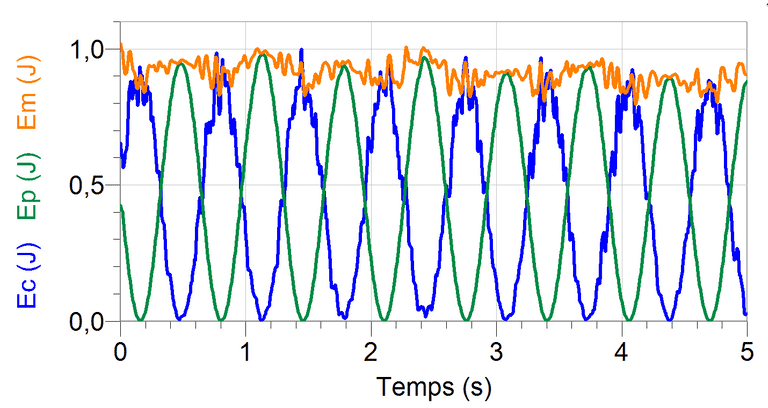
Non conservation de l'énergie mécanique
Dans le cas ou les forces non conservatives travaillent, la variation d'énergie mécanique est égale au travail des forces non conservatives
- Si les forces non conservatives ont un travail résistant:
- Si les forces non conservatives ont un travail moteur:
Pendule amorti: ici les forces de frottement ont un travail résistant.