Programme Officiel
| Contenus | Capacités attendues | Commentaires |
|---|---|---|
| Récursivité. | Écrire un programme récursif. Analyser le fonctionnement d’un programme récursif. |
Des exemples relevant de domaines variés sont à privilégier. |
Dans ce chapitre, nous allons voir comment utiliser des fonctions récursives, des fonctions qui s’appellent elles-mêmes. Ce type de fonction peut avantageusement remplacer la boucle pour écrire des programmes courts et élégants. Ce type de construction est notamment utilisée en programmation fonctionnelle, un paradigme de programmation centrée sur les fonctions.
Définition et exemple
- Fonction récursive
-
Une fonction récursive est une fonction qui s’appelle elle-même dans sa définition.
Commençons par un exemple pour clarifier un peu les choses.
Vous voulez demander à un utilisateur une entrée par exemple son âge, et vous voulez vous assurer que l’utilisateur vous donne bien une valeur entière positive.
On peut implémenter cela avec une boucle while.
age = None
while not(age):
age = int(input("Quel âge avez-vous?"))
if age > 0:
print("Merci pour votre réponse)
# on affecte None à age pour relancer un tour de boucle
print("L'age doit être un entier positif")
age = None
Mais il est aussi tout à fait possible d’utiliser une fonction récursive comme ceci:
def quel_age():
age = int(input("Quel âge avez-vous?"))
if age > 0:
return age
# L'age n'est pas positif, il faut recommencer
print("L'age doit être un entier positif")
# on fait l'appel récursif pour reposer la question
quel_age()
age = quel_age() # appel de la fonction et assignation de la valeur retournée à la variable age
Comme vous le voyez cette fonction continuera de s’appeler tant que nécessaire. On a donc bien remplacé la boucle avec cette fonction.
Gestion des exceptions
Ce code ne traite que le problème du signe, si on voulait être complet il faudrait gérer les problèmes de type(str, float…) avec les structures try except.
Vous pouvez l’implémenter en guise d’exercice.
Comment définir une fonction récursive?
Pour écrire une fonction récursive il faut:
Traiter attentivement le cas récursif du passage des valeurs renvoyées par l’appel précédent à l’appel suivant.
Prévoir le cas de base qui ne nécessite pas de rappel de la fonction afin d’arrêter la boucle.
Nous allons utiliser l’exemple classique de la fonction puissance qui retourne .
Un traitement par une boucle for serait (programmation impérative).
def puissance2(n: int) -> int:
puissance = 1
for i in range(n):
puissance = puissance * 2
return puissance
>>> puissance2(8)
256
Cette fonction peut-être définie par une fonction récursive car:
- Le cas récursif est:
- Le cas de base est:
Voici donc la fonction récursive:
def puissance_recursive(exposant):
# cas de base
if exposant == 0:
return 1
# appel recursif
return 2 * puissance_recursive(exposant - 1 )
puissance_3 = puissance_recursive(3)
Correction de l'algorithme récursif
Nous pouvons démontrer la correction (validité) de cet algorithme, pour cela nous allons prouver par récurrence que .
- Initialisation: pour
,
puissance_recursive(0)vaut 1 qui est bien égal à . - Conservation: si alors .
- Terminaison: L’algorithme se termine, car à chaque tour de boucle
diminue de 1 et on finit par arriver au
returndu cas terminal lorsque à condition d’avoir donné au paramètre une valeur positive à l’appel de la fonction.
Pile d’exécution
Bien que la gestion de la mémoire soit «cachée» au programmeur en Python, qu’il existe deux façons d’allouer de la mémoire à un programme lors de son exécution (on parle d’allocation dynamique).
- Le tas (heap en anglais) est un segment de mémoire que l’on peut faire grandir ou rétrécir à la demande.
- L’autre segment de mémoire utilisé est la pile d’exécution (call stack). La pile sert à enregistrer des informations au sujet des fonctions actives dans un programme informatique, c’est celle qui nous intéresse ici.
Étant donné que la pile d’exécution est une pile, l’appelant pousse l’adresse de retour sur la pile, et la fonction appelée, quand elle se termine, récupère l’adresse de retour au sommet de la pile d’exécution (et y transfère le contrôle). Si une fonction appelée appelle une autre fonction, elle poussera son adresse de retour sur la pile d’exécution. Les adresses de retour s’accumulent donc sur la pile d’exécution et sont récupérées une à une lors de la fin de l’exécution des fonctions. Si l’accumulation des adresses de retour consomme tout l’espace alloué à la pile d’exécution, un message d’erreur appelé un dépassement de pile se produit.
Article Wikipédia sur la pile d’exécution
Pour bien comprendre comment fonctionne la pile d’exécution, on peut exécuter la fonction puissance_recursive pas à pas sur pythontutor.
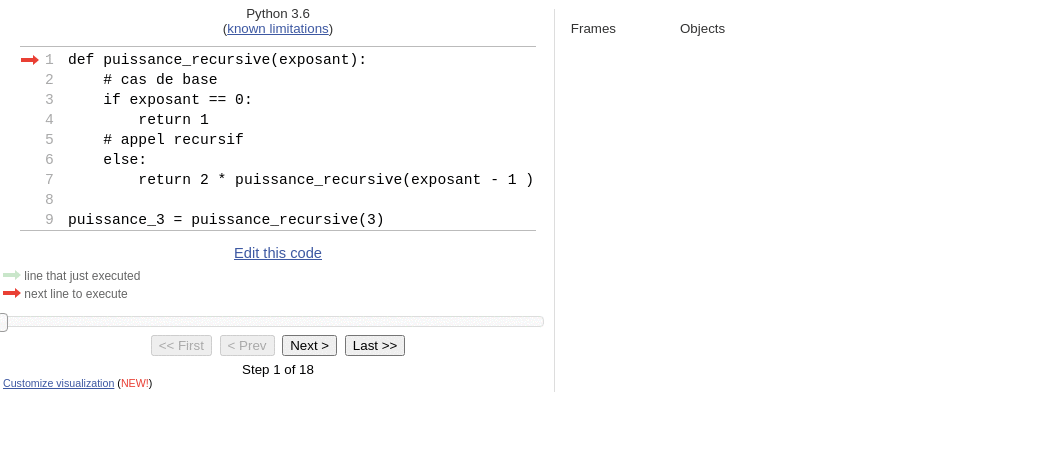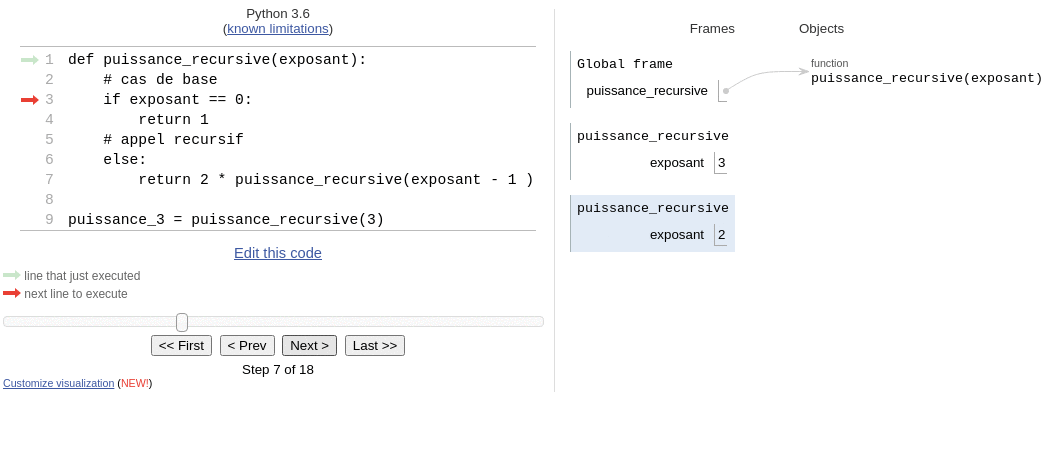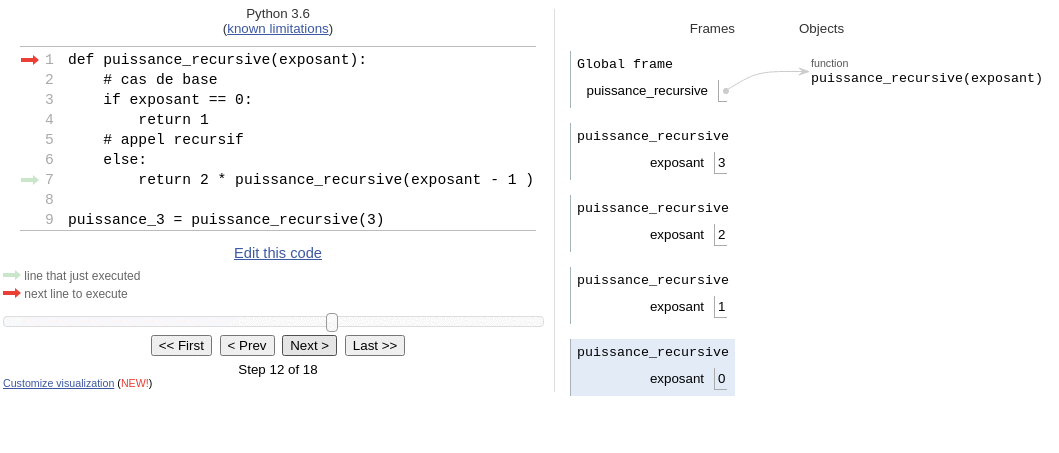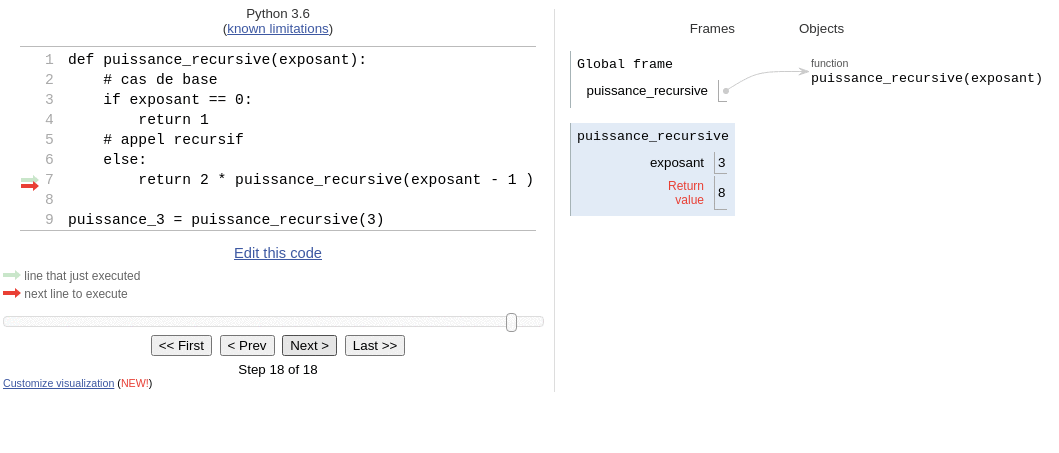
Sur cette animation la pile est «à l’envers»!
Efficacité des algorithmes récursifs
L’écriture d’algorithmes récursifs peut-être très élégante et concise, cependant elle peut avoir des conséquences très néfastes sur leur efficacité. La taille de la pile peut croitre au-dessus des limites de la mémoire, ou encore certains calculs identiques peuvent être réalisés plusieurs fois.
Nous allons voir comment l’utilisation d’un accumulateur peut permettre de passer des valeurs d’un appel à un autre lors de la récursion.
Voici donc la fonction récursive puissance modifiée avec un deuxième paramètre acc ayant pour valeur par défaut 1, et qui accumulera le résultat des multiplications lors des appels récursifs.
def puissance_rec_acc(exposant, acc=1):
# cas de base
if exposant == 0:
return acc
# appel recursif
return puissance_rec_acc(exposant - 1, 2*acc )
puissance_rec_acc(4)
Nous n’avons pas modifié la hauteur de la pile, mais on a modifié l’ordre des opérations effectuées. Les multiplications sont effectuées lors de l’empilement au lieu du dépilement précédemment.
Nous pouvons visualiser l’exécution de cet algorithme sur pythontutor.
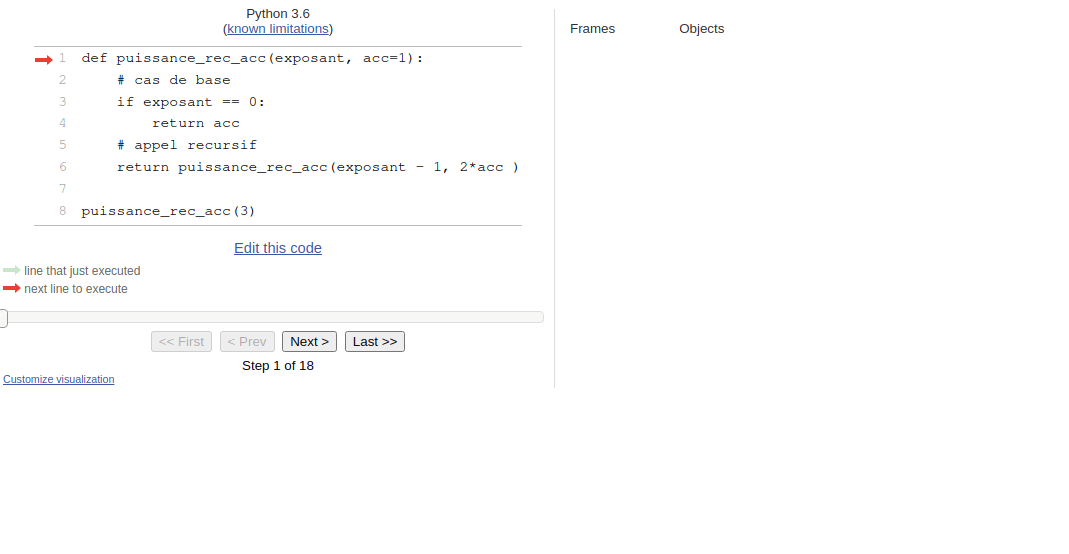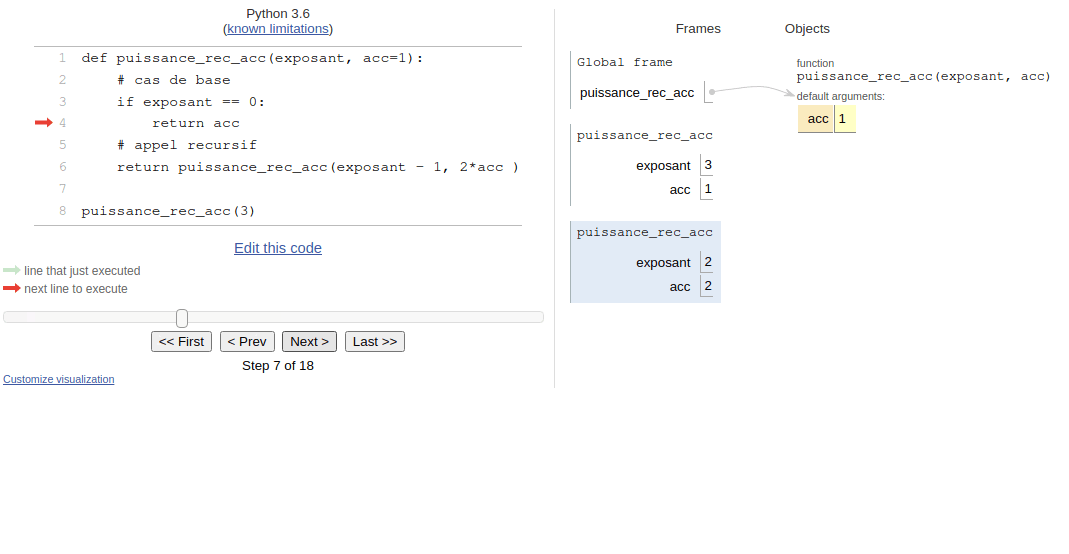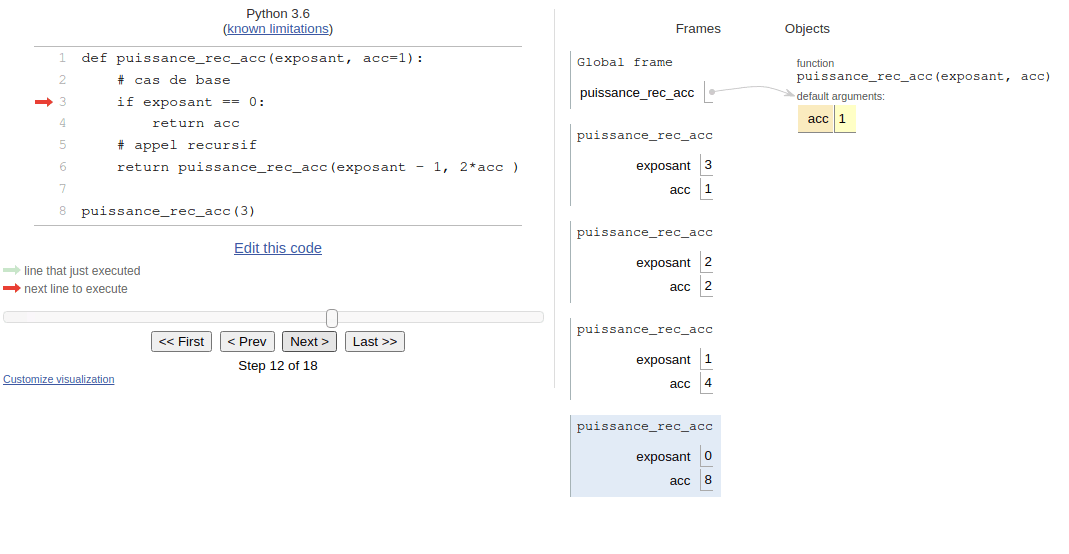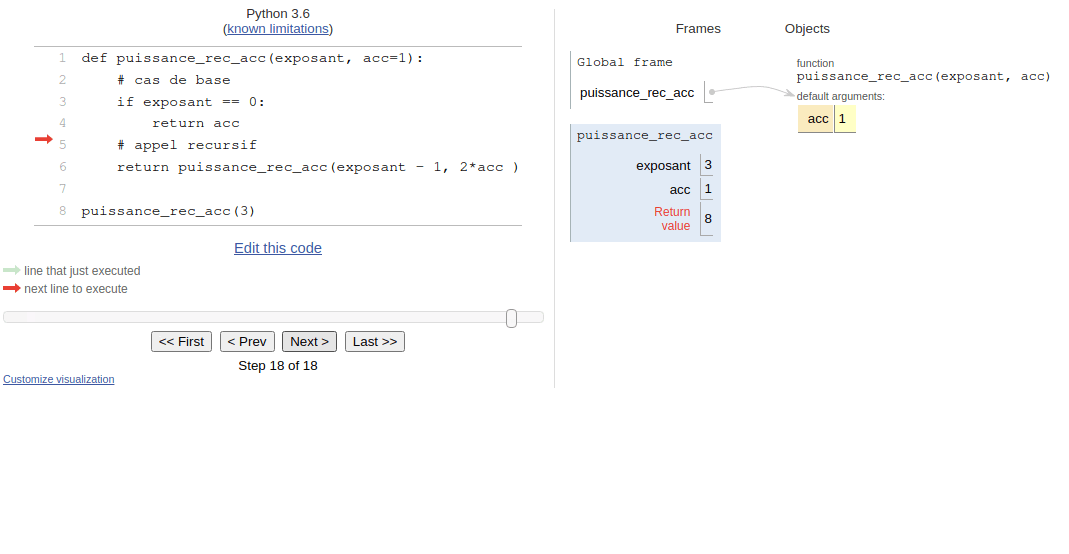
L’utilisation d’un accumulateur est parfois indispensable comme dans les exercices 5 et 6, voire indispensable comme dans le calcul des termes de Fibonacci de grand ordre(exercice 7).