Ce chapitre ne pourra pas faire l’objet d’une évaluation lors de l’épreuve terminale écrite et pratique de l’enseignement de spécialité. BO MENE2121274N
Programme Officiel
| Contenus | Capacités attendues | Commentaires |
|---|---|---|
| Sécurisation des communications. | Décrire les principes de chiffrement symétrique (clef partagée) et asymétrique (avec clef privée/clef publique). Décrire l’échange d’une clef symétrique en utilisant un protocole asymétrique pour sécuriser une communication HTTPS. |
Les protocoles symétriques et asymétriques peuvent être illustrés en mode débranché, éventuellement avec description d’un chiffrement particulier. La négociation de la méthode chiffrement du protocole SSL (Secure Sockets Layer) n’est pas abordée. |
Sécuriser l’échange de données est un aspect crucial lors de l’échange d’informations par exemple lors d’un paiement sur internet. Il existe deux principaux types de chiffrement de données qui permettent de rendre un message lisible uniquement par son destinataire:
- le chiffrement symétrique à clé partagée,
- le chiffrement asymétrique avec une paire clé publique clé privée.
Cryptographie symétrique
La cryptographie symétrique, également dite à clé secrète (par opposition à la cryptographie asymétrique), est la plus ancienne forme de chiffrement. Elle permet à la fois de chiffrer et de déchiffrer des messages à l’aide d’un même mot clé. On a des traces de son utilisation par les Égyptiens vers 2000 av. J.-C.
Article Wikipédia sur la cryptographie symétrique
Cette technique repose sur l’utilisation d’une clé unique qui doit être connue par l’expéditeur et le destinataire.
Il existe de nombreux chiffrements de ce type qui ont évolué en complexité au cours du temps.
Le chiffrement César
On décale les lettres de rangs la clé est tout simplement : le décalage.
Par exemple, César utilisait un décalage de 3 lettres:
Si on connait le décalage, on déchiffre le message en réalisant le décalage opposé, moins trois lettres dans note exemple.
Si on utilise 26 lettres majuscules, il n’existe que 26 clés possibles!
Chiffrement par substitution
On remplace une lettre par une autre de l’alphabet, on a donc clés possibles.
Avec la clé suivante:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
AZERTYUIOPQSDFGHJKLMWXCVBN
le message SUBSTITUTION devient LWZLMOMWMOGF
Chiffrement de Vigenère (XVIe siècle)
Cette méthode a été mise au point durant la renaissance pour contrer la cryptanalyse par la méthode des fréquences de lettres qui permettait de “casser” les clés de cryptage assez facilement.
On choisit une clé sous la forme d’un mot ou d’une phrase qui donne le décalage à appliquer qui devient alors variable.
Supposons que la clé soit ABC, les décalages successifs seront 0, 1, 2, 0, 1, 2, 0…
Avec la clé ABC
Le message SUBSTITUTION devient: SVDSUKTVVIPP
SUBSTITUTION
ABCABCABCABC
------------
SVDSUKTVVIPP
Chiffrement de Vernam (XXe siècle)
Il s’agit d’un système parfaitement sûr, le mathématicien C.Shannon a montré que si on respecte bien les 3 règles de Vernam, ce système est inviolable.
- La clé doit être une suite de caractères au moins aussi longue que le message à chiffrer.
- Les caractères composant la clé doivent être choisis de façon totalement aléatoire.
- Chaque clé, ou « masque », ne doit être utilisée qu’une seule fois (d’où le nom de masque jetable).
Une méthode particulièrement efficace pour traiter le chiffrement et le déchiffrement de messages à partir de la clé est d’utiliser la fonction logique XOR, le ou exclusif qui a une particularité très intéressante dans notre cas.
On note
le message et
la clé secrète, XOR se note
.
On obtient le message chiffré en faisant: .
Le déchiffrement se fait tout simplement en appliquant la même opération car:
On souhaite transmettre le message NSI de façon privée. Le code ASCII correspondant est 01001110 01010011 01001001.
On crée un masque aléatoirement que l’on transmet au destinataire: 11001001 11001101 01100011.
- Ecrire le message chiffré en faisant: .
- Vérifier qu’on déchiffre par la même opération .
Cryptographie asymétrique
La cryptographie asymétrique permet de résoudre le problème de l’échange de la clé secrète.
Elle fut inventée par Whitfield Diffie et Martin Hellman en 1976, qui reçurent le prix Turing de 2015 pour cette découverte.
En cryptographie asymétrique on a 2 clés:
- la clé publique: Celle-ci, tout le monde peut la posséder, il n’y a aucun risque, vous pouvez la transmettre à n’importe qui. Elle sert à chiffrer le message.
- la clé privée: que seul le récepteur possède, en l’occurrence vous. Elle servira à déchiffrer le message chiffré avec la clé publique. Pour clarifier mon charabia, une petite illustration :
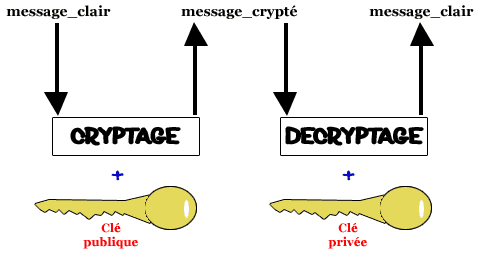
Cours l’algorithme RSA sur OpenClassRoom
Pour que cela fonctionne, il faut que la paire clé publique/clé privée ait une propriété particulière.
Soit la fonction de chiffrement utilisée avec la clé publique, et la fonction relative à la clé privée. Une relation particulière relie ces deux fonctions:
Enfin pour que ce système fonctionne, il faut que:
- la fonction soit facile à calculer pour tout le monde,
- la fonction soit facile à calculer uniquement pour le détenteur de la clé privée.
Un système qui satisfait ces deux critères est le système de chiffrement RSA utilisé pour échanger des données confidentielles sur Internet.
Cet algorithme fut inventé en 1977 par Ronald Rivest, Adi Shamir et Leonard Adleman breveté par le MIT en 1983. Le brevet a expiré le 21 septembre 2000 ce qui permet de l’utiliser librement depuis.
Principe original
Ce système de cryptographie repose sur l’utilisation de nombres premiers et certaines propriétés de l’arithmétique modulaire.
Alice et Bob ont choisi un nombre premier et un nombre strictement plus petit que (ils peuvent aussi, comme montré sur la figure, ne décider de ce choix qu’au moment de l’échange, et se le communiquer en clair, ce qui n’améliore pas les chances d’Ève qui cherche à casser le code)
Alice choisit un nombre au hasard , élève à la puissance , et envoie à Bob le nombre .
De même Bob choisit un nombre au hasard , et fait de même; il transmet le nombre à Alice
En élevant le nombre reçu de Bob à la puissance , obtient .
Bob fait le calcul analogue avec le nombre reçu d’Alice et obtient , qui est le même résultat.
A la fin du protocole, Alice et Bob connaissent tous les deux le nombre mais pas Ève car elle ne peut pas calculer facilement.
Exemple
- Alice et Bob ont choisi un nombre premier et une base . Dans notre exemple, et
- Alice choisit un nombre secret
- Elle envoie à Bob la valeur
- Bob choisit à son tour un nombre secret
- Bob envoie à Alice la valeur
- Alice peut maintenant calculer la clé secrète :
- Bob fait de même et obtient la même clé qu’Alice :
Créez une clé secrète sur ce principe avec votre voisin en Python:
- Choisir ensemble un nombre premier et une base pas trop grands.
- Choisir chacun de votre côté un nombre secret puis calculer .
- Vérifier que chacun peut générer la même clé secrète à partir du nombre calculé par votre voisin.
- Essayez de retrouver la clé à partir des informations échangées en clair: , , et (Ne faites pas cette question, elle est impossible).
Cryptosystèmes hybrides
Bien que le système RSA à clé publique soit a priori sûr et pratique puisqu’il n’est pas nécessaire d’échanger la clé de chiffrement comme dans le cas du chiffrement symétrique. On utilise en pratique plutôt un système hybride, car le système à clé asymétrique est assez lourd à exécuter et prend du temps.
Regardons par exemple le cas d’échange d’informations sécurisées grâce au protocole HTTPS.
- Le client — par exemple le navigateur Web — contacte un serveur — par exemple Wikipédia — et demande une connexion sécurisée.
- Le serveur répond en produisant un certificat qui contient entre autres sa clé publique.
- Cela permet au client d’envoyer de manière secrète une clé symétrique qui sera utilisée à tous les échanges entre le serveur et le client de façon que tous les contenus de la communication — y compris l’adresse même du site web, l’URL — soient chiffrées.
Dans le schéma d’échange de clés Diffie-Hellman, chaque partie génère une paire de clés publique / privée et distribue la clé publique. Après avoir obtenu une copie authentique des clés publiques de chacun, Alice et Bob peuvent calculer une clé secrète partagée hors ligne. La clé secrète partagée peut être utilisée, comme clé pour un chiffrement symétrique.