Chapitre 3: Algorithme des k plus proches voisins
Programme Officiel
| Contenus | Capacités attendues | Commentaires |
|---|---|---|
| Algorithme des k plus proches voisins | Écrire un algorithme qui prédit la classe d'un élément en fonction de la classe majoritaire de ses k plus proches voisins. | Il s'agit d'un exemple d'algorithme d'apprentissage. |
Dans ce chapitre nous abordons un algorithme dit d'apprentissage automatique qui permet à un programme d'apprendre à classer des « objets » en utilisant un jeu de données pour qu'il y trouve des similarités.
C'est un algorithme simple de « machine learning » un sujet très en vogue à l'heure actuelle dans le domaine de l'informatique.
Principe
Principe de l'apprentissage supervisé
A l'heure actuelle, l'intelligence artificielle se base souvent sur l'utilisation de données annotées que l'on fournit à l'ordinateur pour qu'il y trouve des similarités(c'est ce que l'on appele de l'apprentissage supervisé).
On peut fournir à un programme une grande quantité d'écritures de chiffres.
Le programme va lire toutes les données, et grâce à des algorithmes plus
ou moins évolués, le programme va trouver les points communs entre les
chiffres représentant le même nombre.

Ensuite, on peut donner au programme une image non annotée, et il nous dira s'il s'agit d'un 1, d'un 6 ou d'un 8...
C'est un système qui est utilisé depuis des années pour la lecture des codes postaux sur les lettres avec un efficacité supérieure à 99%.
Principe l'algorithme des k plus proches voisins
On dispose d'une collection de données annotées, et on veut savoir à quelle catégorie appartient un nouvel échantillon. Il s'agit d'un problème de classification.
Prenons l'exemple suivant issu de cette page.
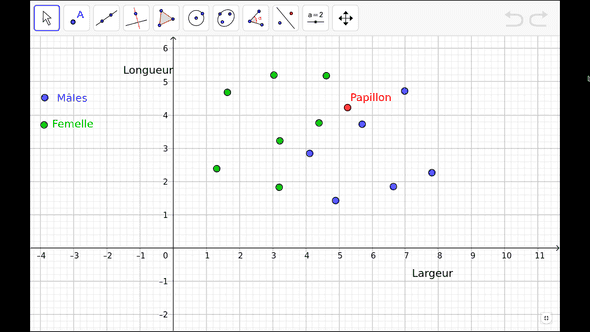
Imaginons... On étudie des papillons. Ceux-ci ont une certaine largeur et une certaine longueur. Certains sont des males, d'autres des femelles.
On étudie un certain nombre de ces papillons. Cela constitue un jeu d'apprentissage dont les caractéristiques sont représentées ci-dessous.
A partir de ce jeu d'apprentissage, on cherche à prédire le sexe d'un papillon dont on connaît les dimensions.
L'objectif est maintenant d'identifier le sexe d'un nouveau papillon en s'appuyant sur notre expérience précédente.
Le principe est simple : On fait l'hypothèse que notre papillon a le même sexe que ces voisins.
On voit par exemple que le voisin le plus proche est un paillon mâle:
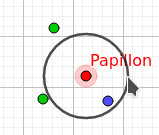
Cependant la particularité de l'algorithme des k plus proches voisins est le fait que l'on puisse choisir , le nombre de plus proches voisins nous permettant de faire notre choix, on va prendre plusieurs voisins pour éviter de se baser que sur une observation pour notre choix.
Voici par exemple l'application pour :
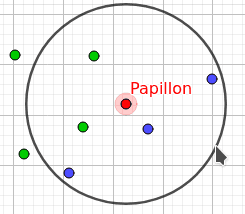
Influence du nombre de voisins
En utilisant ce fichier geogebra montrer comment le choix de a une influence sur la prévision de la méthode.
Implémentation naïve en Python
Le code qui suit utilise des méthodes de pandas matplotlib et
numpy non vues, il n'est pas nécessaire de savoir le refaire, par
contre en utilisant les commentaires vous pouvez voir comment est
effctuée la classification dans cet implémentation.
Classification d'élèves en conseil de classe
Nous allons utiliser un fichier csv qui contient les moyennes,
absences et mentions d'élèves de lycée.
Vous pouvez visualiser ce fichier ici: https://framagit.org/lyceum/k-plus-proches-voisins/blob/master/data/mentions-anonymised.csv
A partir de ce fichier de données l'algorithme sera capable de vous indiquer quelle sera votre mention (Félicitations, compliments...) en fonction de notre moyenne générale et notre nombre d'absences.
Tracé de la classification
Commencons par observer l'ensemble des données sous forme graphique pour se faire une idée.
Entrée
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as npEntrée
# données du conseil de classe
df = pd.read_csv('./data/mentions-anonymised.csv')
# On affiche 3 échantillons du tableau
df.sample(3)Résultat
| Mentions | 1/2j abs | Rang | Moyenne Générale | PHILOSOPHIE | HISTOIRE-GEOGRAPHIE | MATHEMATIQUES | PHYSIQUE-CHIMIE | SCIENCES VIE & TERRE | ED.PHYSIQUE & SPORT. | ... | ESPAGNOL LV2 | ITALIEN LV2 | JAPONAIS LV2 | SPECIALITE SVT | SPECIALITE PHYS | NISSART LV3 | SPECIALITE MATHS | SPECIALITE ISN | arts fac | ENS. MORAL & CIVIQUE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 59 | Encouragements | 16.0 | 20.0 | 12.1 | 13.5 | NaN | 12.4 | 9.0 | 11.0 | 18.0 | ... | NaN | 12.1 | NaN | NaN | NaN | N.Not | 13.7 | NaN | NaN | NaN |
| 9 | Félicitations | 9.0 | 3.0 | 17.8 | 18.5 | 18.5 | 18.9 | 20.0 | 17.6 | 12.0 | ... | NaN | 17.3 | NaN | NaN | 16.3 | 18.7 | NaN | NaN | NaN | NaN |
| 68 | Encouragements | 2.0 | 24.0 | 12.3 | 13.7 | 12.5 | 12.4 | 11.5 | 12.0 | 15.5 | ... | NaN | 14.5 | NaN | 11.1 | NaN | 16.9 | NaN | NaN | NaN | 14.0 |
3 rows × 22 columns
Entrée
# on ne conserve que 3 colonnes pour cette étude simplifiée
df = df.loc[:, ['Moyenne Générale', '1/2j abs', 'Mentions']]
dfRésultat
| Moyenne Générale | 1/2j abs | Mentions | |
|---|---|---|---|
| 0 | 17.4 | 3.0 | Félicitations |
| 1 | 18.1 | 5.0 | Félicitations |
| 2 | 18.2 | NaN | Félicitations |
| 3 | 17.0 | 1.0 | Félicitations |
| 4 | 17.6 | 2.0 | Félicitations |
| ... | ... | ... | ... |
| 91 | 9.0 | 12.0 | Encouragements |
| 92 | 9.4 | 14.0 | Pas de mention |
| 93 | 7.7 | 49.0 | Pas de mention |
| 94 | 12.3 | 32.0 | Pas de mention |
| 95 | 11.7 | 33.0 | Pas de mention |
96 rows × 3 columns
Entrée
def tracé_graph():
for mention in ["Pas de mention","Encouragements", "Compliments", "Félicitations"]:
df_mention = df.loc[df["Mentions"] == mention]
plt.scatter(df_mention["1/2j abs"], df_mention["Moyenne Générale"], label=mention, alpha=0.5)
plt.legend()
tracé_graph()
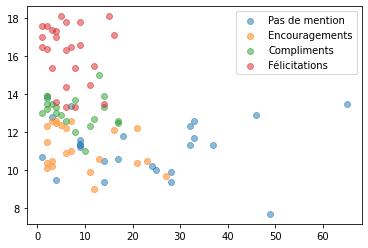
On voit bien le groupe des Félicitations se dégager avec des hautes notes et peu d'absences, ainsi que le groupe Pas de mention pour les absentéistes. Par contre la zone basse du graphique présente de nombreux points de divers mentions proches.
Implémentation de l'algorithme
Nous allons maintenant définir la fonction qui à partie de la moyenne et des absences données en argument renverra la mention des k plus proches voisins(par défaut: 3).
Entrée
def k_plus_proches_voisins(moyenne, absences, k=3):
"""Renvoie la classe des k plus proches voisins
Entrée:
moyenne: moyenne de l'élève
absences: nb de 1/2j d'absences lors du trimestre
k: nombre de voisins les plus proches à utiliser(par défaut 3)
Sortie:
renvoie les classe la plus probable des k plus porches voisins"""
# on commence par afficher notre point sur un graphique
plt.scatter(absences, moyenne, label="Elève étudié", marker="P")
# on crée une liste pour stocker les distances euclidiennes
df['distance'] = df.apply(lambda row: ((row["Moyenne Générale"] - moyenne)**2 + (row["1/2j abs"] - absences)**2)**0.5, axis=1)
# On affiche les trois plus courtes distances
df_voisins = df.iloc[df.distance.sort_values().index[:k]]
print(df_voisins)
# on les marque sur le graph
plt.scatter(df_voisins["1/2j abs"],
df_voisins["Moyenne Générale"],
label="Plus proches voisins", marker="*")
# On ajoute tous les autres points
tracé_graph()
return df_voisins["Mentions"].value_counts().nlargest(1)Appels de la fonction
Entrée
k_plus_proches_voisins(12.5, 10)Sortie
Moyenne Générale 1/2j abs Mentions distance
32 12.3 11.0 Compliments 1.019804
62 11.6 9.0 Pas de mention 1.345362
66 11.4 9.0 Pas de mention 1.486607Résultat
Pas de mention 2
Name: Mentions, dtype: int64
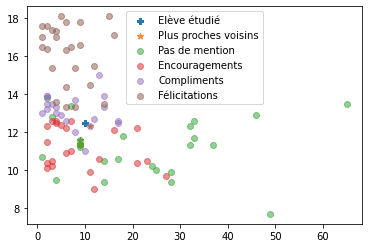
On observe donc que l'élève n'aurait pas de mention malgré ses 12.5 de moyenne, Voyons ce qu'il en est si on réduit le nombre d'absences à 5.
Entrée
k_plus_proches_voisins(12.5, 5)Sortie
Moyenne Générale 1/2j abs Mentions distance
65 12.4 5.0 Encouragements 0.1
46 12.9 5.0 Compliments 0.4
58 12.5 4.0 Encouragements 1.0Résultat
Encouragements 2
Name: Mentions, dtype: int64
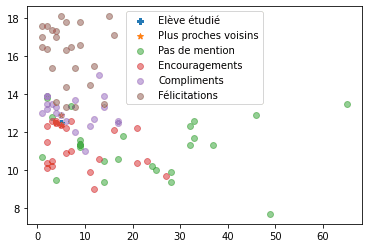
L'élève a maintenant les encouragements.
Et vous, quelle serait votre mention?
L'algorithme et les données sont en ligne dans le dépôt suivant:
https://framagit.org/lyceum/k-plus-proches-voisins
Vous pouvez soit télécharger le dossier pour travailler sur le code sur votre machine si vous avaez installé python et anconda chez vous.
Vous pouvez sinon travailler en ligne en lancant un environment
.
L'algorithme est-il efficace?
Reprendre vos bulletins de lycée pour vérifier si la prévision faite à partir de votre moyenne générale et de votre nombre de jours d'absences est conforme au résultat obtenu.
Vous pouvez éventuellement changer la valeur de pour améliorer les prédictions.
Pour conclure: Que diriez-vous de cette méthode? Peut-on vraiment qualifier cet algorithme d'intelligence artificielle? Voyez-vous des dangers à la prise de décisions par des algorithmes?
Notes sur l'algorithme
Cet algorithme(brute-force) est peu efficace avec une complexité de (voir doc sklearn).
D'autres part, il serait bon de mettre à l'échelle les données utilisées, car on voit bien que l'échelle des absences est trois fois plus grande que les moyennes, et ainsi a un importance accrue dans le calcul de la distance des voisins.
Références
-
Cours de Nadja Rebinguet duquel est extrait l'exemple des papillons: https://nadjarebinguet.wordpress.com/2020/03/20/algorithme-des-k-plus-proches-voisins/
-
Cette video de Phillippe Bouchery sur le machine learning
-
Cours sur pixees.fr: https://pixees.fr/informatiquelycee/n_site/nsi_prem_knn.html
-
Article Wikipedia: https://fr.wikipedia.org/wiki/M%C3%A9thode_des_k\_plus_proches_voisins
-
Doc sklearn: https://scikit-learn.org/stable/modules/neighbors.html#nearest-neighbor-algorithms