Programme Officiel
| Contenus | Capacités attendues | Commentaires |
|---|---|---|
| Mise au point de programmes | Utiliser des jeux de tests. |
L'importance de la qualité et du nombre des tests est mise en évidence. Le succès d'un jeu de tests ne garantit pas la correction d'un programme. |
| Utilisation de bibliothèques | Utiliser la documentation d'une bibliothèque. | Aucune connaissance exhaustive d'une bibliothèque particulière n'est exigible. |
Nous avons déjà vu que parmi des ingrédients des programmes, il y en a un qui est particuliérément utile pour rendre les programmes plus lisibles et structurés et donc plus faciles à maintenir, c'est l'utilisation de fonctions.
Nous avons également vu comment prototyper des fonctions afin de pouvoir rendre le code plus explicite et que l'on puisse revenir dessus afin de l'améliorer ou le corriger plus tard lors du développement du programme.
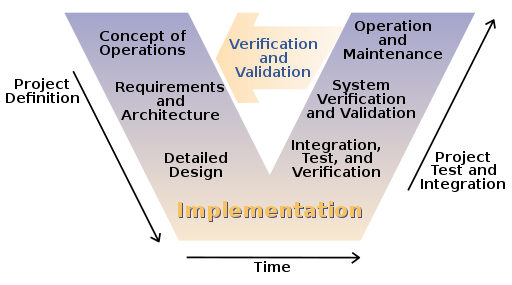
Nous étions alors dans la phase descendante de la conception du programme qui nous a permis d'arriver à implémenter notre programme. Ce modèle d'organisation de la conception d'un programme est connu sous le nom de cycle en V, et il est un standard utuilisé depuis les années 1980.
Nous allons voir dans ce chapitre une autre étape du cycle de développement d'applications: La mise au point du programme grâce à l'utilisation de tests.
Prenons l'exemple du calcul des racines du trinôme proposé par un élève. Nous allons peu à peu améliorer ce programme pour le rendre plus stable, plus facile à utiliser, à maintenir et à améliorer pour le futur.
import math
print("""
Programme de calcul des racines d'un trinôme
============================================
ax^2 + bx +c
""")
a = float(input("Entrer la valeur de a: "))
b = float(input("Entrer la valeur de b: "))
c = float(input("Entrer la valeur de c: "))
# Calcul du discriminant
delta = b * b - 4 * a * c;
# Affichage des solutions
if delta < 0:
print("Pas de solution")
elif delta == 0:
print("Une solution : ",end="")
print(- b / (2 * a))
else:
print("Deux solutions : ",end="")
print((- b - math.sqrt(delta)) / (2 * a),end="")
print(" et ",end="")
print((- b + math.sqrt(delta)) / (2 * a))Utilisation d'une approche fonctionnelle: def
Plutôt que de placer les instructions les unes à la suite des autres sans réelle organisation, nous allons utiliser une approche fonctionnelle pour rendre ce programme plus pratique à utiliser et à tester.
La programmation fonctionnelle est un paradigme de programmation très apprécié notamment dans le monde universitaire, et de plus en plus utilisé par l'industrie afin d'avoir des programmes dont le comportement est plus facile à prédire que dans un programmation orientée objet par exemple.
On va placer le code dans une fonction qui prend trois arguments, les coefficients du trinôme et qui affiche les racines à l'écran(il s'agit pour l'instant d'une procédure).
Entrée
def racines_du_trinome(a, b, c):
import math
# Calcul du discriminant
delta = b * b - 4 * a * c
# Affichage des solutions
if delta < 0:
print("Pas de solution")
elif delta == 0:
print("Une solution : ",end="")
print(- b / (2 * a))
else:
print("Deux solutions : ",end="")
print((- b - math.sqrt(delta)) / (2 * a),end="")
print(" et ",end="")
print((- b + math.sqrt(delta)) / (2 * a))
racines_du_trinome(a=1, b=0, c=-1)Sortie
Deux solutions : -1.0 et 1.0Renvoi de valeurs: return
Nous allons maintenant remplacer les print par des return pour
récupérer les racines en sortie de la fonction.
En effet tout ce qui se passe à l'intérieur d'une fonction reste à
l'intérieur de la fonction, mais par contre les print() sont des
fonctions globales qui agissent à l'extérieur de la fonction( On parle
d'effets de bords).
En utilisant des return, on pourra récupérer le résultat de l'algorithme de notre fonction que lorsqu'on l'appelera, et qu'on assignera éventuellemnt ces valeurs de retour à des variables(globales ou non).
Entrée
def racines_du_trinome(a, b, c):
import math
# Calcul du discriminant
delta = b * b - 4 * a * c
# Affichage des solutions
if delta < 0:
return ()
elif delta == 0:
return (- b / (2 * a))
else:
r1 = (- b - math.sqrt(delta)) / (2 * a)
r2 = (- b + math.sqrt(delta)) / (2 * a)
return (r1, r2)
racines_du_trinome(a=1, b=0, c=-1)Résultat
(-1.0, 1.0)Prototypage de la fonction
Pour rendre notre code compréhensible et facile à maintenir, on va écrire le prototype de la fonction comme on l'a vu dans le chapitre sur fonctions.
On appelle cela une
docstring
qui permet de comprendre comment "fonctionne" la fonction.
On la place sur une chaine de caractères multi-line avec trois guillemets. Elle se présente généralement en trois parties:
- Une explication
- Paramètres
- Sortie(Returns en anglais)
Même si Python est un lagage non typé, on précise les type des paramètres et sorties de la fonction.
La docstring peut alors être renvoyée en cas de besoin avec la fonction
Python help(nom_de_la_fonction)
Entrée
def racines_du_trinome(a, b, c):
"""Renvoie les éventuelles racines d'un trinôme
ax**2 + bx + c
Parameters
----------
a : float
b : float
c : float
Returns
-------
tuple
tuple contenant les 0, 1 ou 2 racines du trinôme suivant le cas
"""
import math
# Calcul du discriminant
delta = b * b - 4 * a * c
# Affichage des solutions
if delta < 0:
return ()
elif delta == 0:
return (- b / (2 * a))
else:
r1 = (- b - math.sqrt(delta)) / (2 * a)
r2 = (- b + math.sqrt(delta)) / (2 * a)
return (r1, r2)
help(racines_du_trinome)Sortie
Help on function racines_du_trinome in module __main__:
racines_du_trinome(a, b, c)
Renvoie les éventuelles racines d'un trinôme
ax**2 + bx + c
Parameters
----------
a : float
b : float
c : float
Returns
-------
tuple
tuple contenant les 0, 1 ou 2 racines du trinôme suivant le casLes tests: assert
L'informatique consiste la plupart du temps à une chasse aux bugs, il convient donc d'essayer de les repérer le plus tôt possible à l'aide de tests.
On va donc pour effectuer des tests sur les valeurs renvoyées par la
fonction. Pour cela on utilise des assertions assert qui bloquent
l'éxecution du programme lorsqu'une expression renvoie False.
On va placer ces tests dans une fonction appelée run_tests() pour
pouvoir en placer plusieurs au fur et à mesure qu'on y pense ou que l'on
constate des bugs.
Entrée
def run_tests():
# deux racines réelles
assert racines_du_trinome(1,0,-1) == (-1.0, 1.0)
# une racine double
assert racines_du_trinome(1, 0, 0) == (0.0)
# pas de racine
assert racines_du_trinome(1, 0, 1) == ()
# si une assertion s'avère fausse la fonction va renvoyer une AssertionError
print("Tous les tests ont été passé avec succés")
run_tests()Sortie
Tous les tests ont été passé avec succésLes bibliothèques: import
Les bibliothéques ou modules permettent de rassembler et d'organiser
les diverses fonctionnalités d'un programme afin de pouvoir les
importer ultérieurement.
Elles constituent un outil important dans la mise au point de programme complexe en permettant de séparer le code en diveres parties, chacune de ces parties ayant un rôle bien spécifique et plus facile à tester.
De nombreuses bibliothéques sont fournies avec Python, comme par exemple
les modules math ou random. On les appelle les bibilothèques
standards. On en a également utilisé d'autres non fournies avec Python,
mais facilement installables comme pandas pour le traitement de
données, ou matplotlib pour le tracé de graphiques.
Entrée
import math
# racine carré de 4
math.sqrt(4)Résultat
2.0Entrée
import random
# nombre aléatoire entre 0 et 1
random.random()Résultat
0.5463364268335839On peut accéder à la documentation directement à partir de python avec
la fonction help, mais on préférera tout de même la documentation en
ligne lorsqu'on a accès à internet.
- Doc Python: https://docs.python.org/3/
- Doc javascript: https://developer.mozilla.org/fr/docs/Web/JavaScript
Entrée
help(math)Sortie
Help on module math:
NAME
math
MODULE REFERENCE
https://docs.python.org/3.8/library/math
The following documentation is automatically generated from the Python
source files. It may be incomplete, incorrect or include features that
are considered implementation detail and may vary between Python
implementations. When in doubt, consult the module reference at the
location listed above.
DESCRIPTION
This module provides access to the mathematical functions
defined by the C standard.
FUNCTIONS
acos(x, /)
Return the arc cosine (measured in radians) of x.
acosh(x, /)
Return the inverse hyperbolic cosine of x.
asin(x, /)
Return the arc sine (measured in radians) of x.
asinh(x, /)
Return the inverse hyperbolic sine of x.
atan(x, /)
Return the arc tangent (measured in radians) of x.
atan2(y, x, /)
Return the arc tangent (measured in radians) of y/x.
Unlike atan(y/x), the signs of both x and y are considered.
atanh(x, /)
Return the inverse hyperbolic tangent of x.
ceil(x, /)
Return the ceiling of x as an Integral.
This is the smallest integer >= x.
comb(n, k, /)
Number of ways to choose k items from n items without repetition and without order.
Evaluates to n! / (k! * (n - k)!) when k <= n and evaluates
to zero when k > n.
Also called the binomial coefficient because it is equivalent
to the coefficient of k-th term in polynomial expansion of the
expression (1 + x)**n.
Raises TypeError if either of the arguments are not integers.
Raises ValueError if either of the arguments are negative.
copysign(x, y, /)
Return a float with the magnitude (absolute value) of x but the sign of y.
On platforms that support signed zeros, copysign(1.0, -0.0)
returns -1.0.
cos(x, /)
Return the cosine of x (measured in radians).
cosh(x, /)
Return the hyperbolic cosine of x.
degrees(x, /)
Convert angle x from radians to degrees.
dist(p, q, /)
Return the Euclidean distance between two points p and q.
The points should be specified as sequences (or iterables) of
coordinates. Both inputs must have the same dimension.
Roughly equivalent to:
sqrt(sum((px - qx) ** 2.0 for px, qx in zip(p, q)))
erf(x, /)
Error function at x.
erfc(x, /)
Complementary error function at x.
exp(x, /)
Return e raised to the power of x.
expm1(x, /)
Return exp(x)-1.
This function avoids the loss of precision involved in the direct evaluation of exp(x)-1 for small x.
fabs(x, /)
Return the absolute value of the float x.
factorial(x, /)
Find x!.
Raise a ValueError if x is negative or non-integral.
floor(x, /)
Return the floor of x as an Integral.
This is the largest integer <= x.
fmod(x, y, /)
Return fmod(x, y), according to platform C.
x % y may differ.
frexp(x, /)
Return the mantissa and exponent of x, as pair (m, e).
m is a float and e is an int, such that x = m * 2.**e.
If x is 0, m and e are both 0. Else 0.5 <= abs(m) < 1.0.
fsum(seq, /)
Return an accurate floating point sum of values in the iterable seq.
Assumes IEEE-754 floating point arithmetic.
gamma(x, /)
Gamma function at x.
gcd(x, y, /)
greatest common divisor of x and y
hypot(...)
hypot(*coordinates) -> value
Multidimensional Euclidean distance from the origin to a point.
Roughly equivalent to:
sqrt(sum(x**2 for x in coordinates))
For a two dimensional point (x, y), gives the hypotenuse
using the Pythagorean theorem: sqrt(x*x + y*y).
For example, the hypotenuse of a 3/4/5 right triangle is:
>>> hypot(3.0, 4.0)
5.0
isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)
Determine whether two floating point numbers are close in value.
rel_tol
maximum difference for being considered "close", relative to the
magnitude of the input values
abs_tol
maximum difference for being considered "close", regardless of the
magnitude of the input values
Return True if a is close in value to b, and False otherwise.
For the values to be considered close, the difference between them
must be smaller than at least one of the tolerances.
-inf, inf and NaN behave similarly to the IEEE 754 Standard. That
is, NaN is not close to anything, even itself. inf and -inf are
only close to themselves.
isfinite(x, /)
Return True if x is neither an infinity nor a NaN, and False otherwise.
isinf(x, /)
Return True if x is a positive or negative infinity, and False otherwise.
isnan(x, /)
Return True if x is a NaN (not a number), and False otherwise.
isqrt(n, /)
Return the integer part of the square root of the input.
ldexp(x, i, /)
Return x * (2**i).
This is essentially the inverse of frexp().
lgamma(x, /)
Natural logarithm of absolute value of Gamma function at x.
log(...)
log(x, [base=math.e])
Return the logarithm of x to the given base.
If the base not specified, returns the natural logarithm (base e) of x.
log10(x, /)
Return the base 10 logarithm of x.
log1p(x, /)
Return the natural logarithm of 1+x (base e).
The result is computed in a way which is accurate for x near zero.
log2(x, /)
Return the base 2 logarithm of x.
modf(x, /)
Return the fractional and integer parts of x.
Both results carry the sign of x and are floats.
perm(n, k=None, /)
Number of ways to choose k items from n items without repetition and with order.
Evaluates to n! / (n - k)! when k <= n and evaluates
to zero when k > n.
If k is not specified or is None, then k defaults to n
and the function returns n!.
Raises TypeError if either of the arguments are not integers.
Raises ValueError if either of the arguments are negative.
pow(x, y, /)
Return x**y (x to the power of y).
prod(iterable, /, *, start=1)
Calculate the product of all the elements in the input iterable.
The default start value for the product is 1.
When the iterable is empty, return the start value. This function is
intended specifically for use with numeric values and may reject
non-numeric types.
radians(x, /)
Convert angle x from degrees to radians.
remainder(x, y, /)
Difference between x and the closest integer multiple of y.
Return x - n*y where n*y is the closest integer multiple of y.
In the case where x is exactly halfway between two multiples of
y, the nearest even value of n is used. The result is always exact.
sin(x, /)
Return the sine of x (measured in radians).
sinh(x, /)
Return the hyperbolic sine of x.
sqrt(x, /)
Return the square root of x.
tan(x, /)
Return the tangent of x (measured in radians).
tanh(x, /)
Return the hyperbolic tangent of x.
trunc(x, /)
Truncates the Real x to the nearest Integral toward 0.
Uses the __trunc__ magic method.
DATA
e = 2.718281828459045
inf = inf
nan = nan
pi = 3.141592653589793
tau = 6.283185307179586
FILE
/usr/lib/python3.8/lib-dynload/math.cpython-38-x86_64-linux-gnu.soBibliothèques tierces
Le succés d'un langage viendra souvent des bibliothèques tiers qui seront développées autour de lui, on télécharge aujourd'hui les bibliotgèques open-source directement sur internet.
- modules Python: https://pypi.org/
- modules javascript: https://www.npmjs.com/
En effet nous sommes souvent ammenés à réaliser le même type de tâches pour concevoir notre programme, et il n'est pas nécessaire de repartir de zéro à chaque fois.