Vous êtes sur une version archivée de lyceum.fr de l'année 2020/2021. Revenir au présent.

Chapitre 4: Récursivité

Plan

Définition et exemple
Comment définir une fonction récursive?

Programme Officiel

Contenus

Capacités attendues

Commentaires

Récursivité.

Écrire un programme récursif.

Analyser le fonctionnement d’un programme récursif.

Des exemples relevant de domaines variés sont à privilégier.

Lien vers le programme complet

Dans ce chapitre, nous allons voir comment utiliser des fonctions récursives, des fonctions qui s'appellent elles-mêmes. Ce type de fonction peut avantageusement remplacer la boucle pour écrire des programmes courts et élégants. Ce type de construction est notamment utilisée en programmation fonctionnelle, un paradigme de programmation centrée sur les fonctions.

Définition et exemple

Fonction récursive

Commençons par un exemple pour clarifier un peu les choses.

Vous voulez demander à un utilisateur une entrée par exemple son âge, et vous voulez vous assurer que l'utilisateur vous donne bien une valeur entière positive.

On peut implémenter cela avec une boucle while.

age = None
while not(age):
    age = int(input("Quel âge avez-vous?"))
    if age > 0:
        print("Merci pour votre réponse)
    else:
        print("L'age doit être un entier positif")
        age = None

Mais il est aussi tout à fait possible d'utiliser une fonction récursive comme ceci:

def quel_age():
    """Demande à un utilisateur son âge
    
    et lui demande de façon récursive tant 
    qu'il n'a pas donné un entier supérieur à 0
    
    Returns
    -------
    int
    """
    age = int(input("Quel âge avez-vous?"))
    if age > 0:
        return age
    else:
        print("L'age doit être un entier positif")
        # on fait l'appel récursif en cas d'erreur
        quel_age()

age = quel_age() # appel de la fonction et assignation de la valeur retournée à la variable age

Gestion des exceptions

Ce code ne traite que le problème du signe, si on voulait être complet il faudrait gérer les problèmes de type(str, float...) avec les structures try except.

Vous pouvez l'implémenter en guise d'exercice.

Comme vous le voyez cette fonction continuera de s'appeler tant que nécessaire. On a donc bien remplacé la boucle avec cette fonction.

Comment définir une fonction récursive?

Pour écrire une fonction récursive il faut:

Commencer par prévoir le cas de base qui ne nécessite pas de rappel de la fonction.
Traiter attentivement le cas récursif du passage des valeurs renvoyées par l'appel précédent à l'appel suivant.

Nous allons utiliser l'exemple classique de la fonction puissance qui retourne $2^n$ .

Cette fonction peut-être définie par une fonction récursive car:

$2^n = 2 * 2^{n-1}$
Le cas de base étant: $2^0 = 1$

Voici donc la fonction récursive:

def puissance_recursive(exposant):
    # cas de base
    if exposant == 0:
        return 1
    # appel recursif
    else:
        return 2 * puissance_recursive(exposant - 1 )

puissance_3 = puissance_recursive(3)

Pour bien comprendre la chaîne d'exécution de cette fonction on peut l'exécuter pas à pas sur pythontutor.

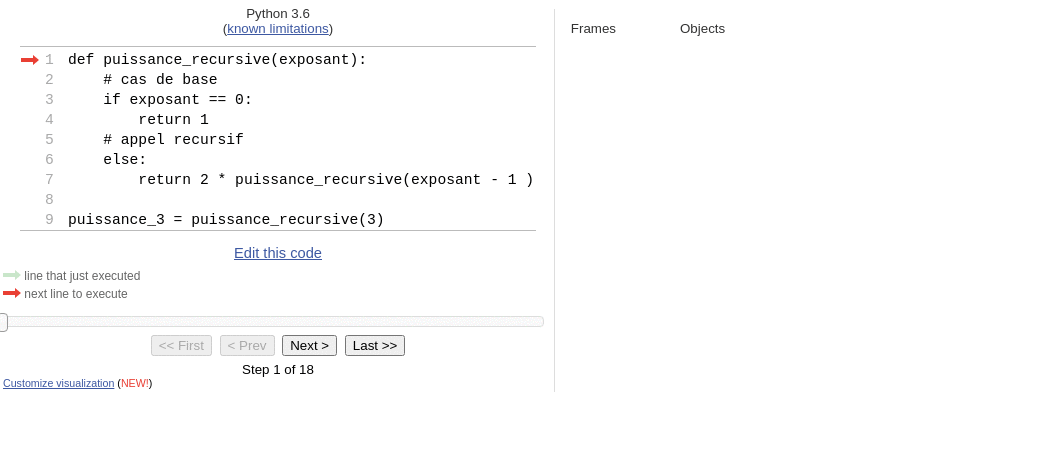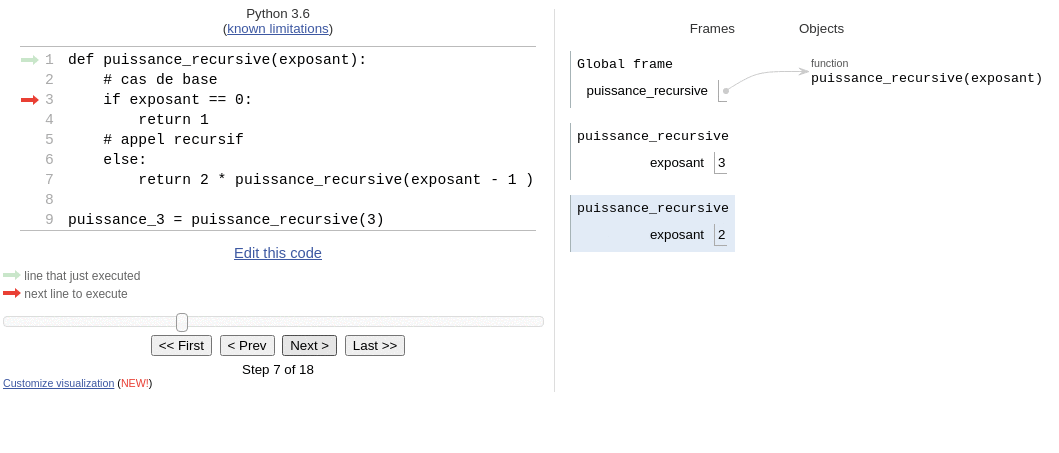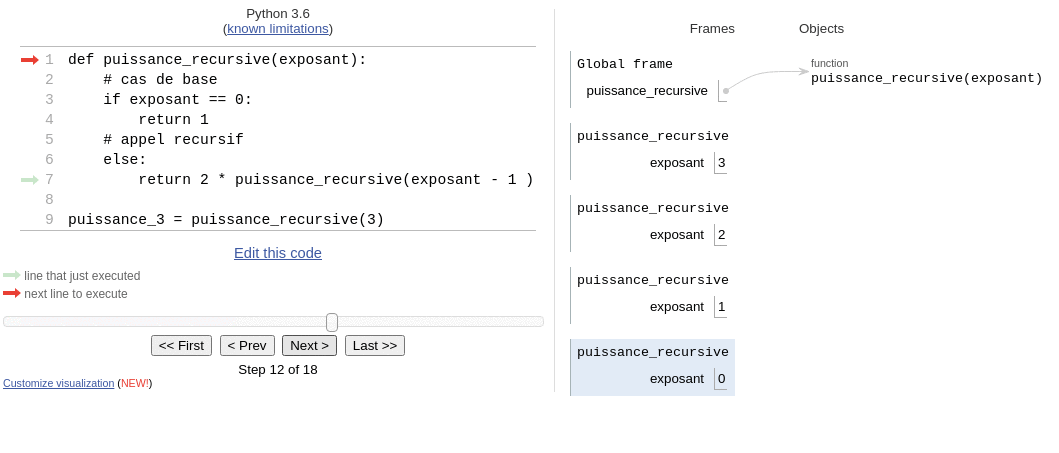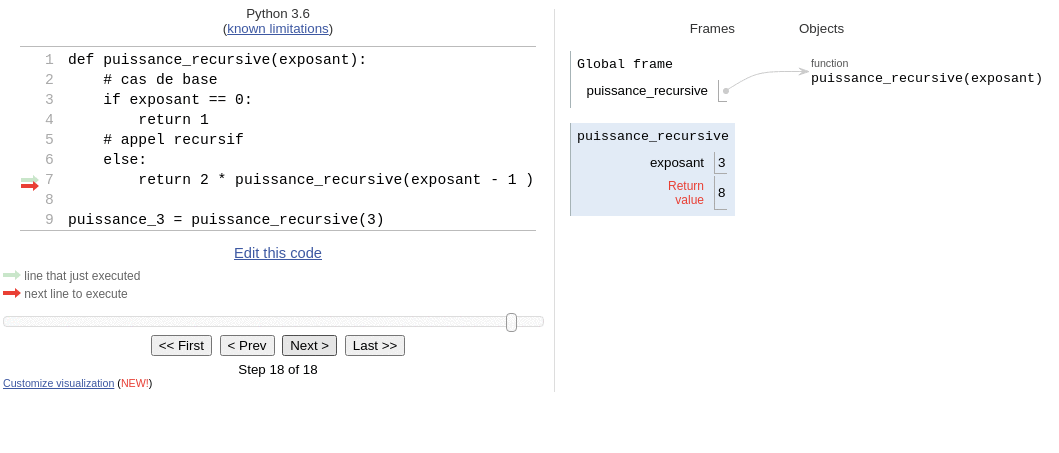
Animation appel récursif sur python tutor

Nous pouvons démontrer la correction(ou validité) de cet algorithme, pour cela nous allons prouver par récurrence que $puissance recursive(n) = 2^n$ .

Initialisation: pour $exposant = 0$ , puissance_recursive(0) vaut 1 qui est bien égal à $2^0$ .
Conservation: si $puissance recursive(n-1) = 2^{n-1}$ alors $puissance recursive(n) = 2 \times puissance recursive(n-1) = 2\times2^{n-1}=2^n$ .
Terminaison: L'algorithme se termine car à chaque tour de boucle $n$ diminue de 1 et on fini par arriver au return du cas terminal lorsque $n=0$ si on a fourni initialement un argument positif pour n.