Programme Officiel
Contenus | Capacités attendues | Commentaires |
|---|---|---|
Arbres : structures hiérarchiques. Arbres binaires : nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits. | Identifier des situations nécessitant une structure de données arborescente. Évaluer quelques mesures des arbres binaires (taille, encadrement de la hauteur, etc.). | On fait le lien avec la rubrique « algorithmique ». |
Image par Birger Eriksson — Travail personnel, CC BY-SA 3.0, Lien
Dans ce chapitre, on présente une nouvelle structure de donnée: les arbres qui sont particulièrement adaptés à la représentation des données hiérarchiques comme un arbre généalogique ou encore le DOM d'une page
html.
Vocabulaire
Un arbre est constitué de nœuds reliés par des arêtes. Souvent les nœuds ont une valeur: l'étiquette.
Un arbre enraciné (ou arborescence) possède à sa base une racine auxquels sont reliés d'autres nœuds qui sont ses descendants.
.svg#/media/File:Tree_(computer_science).svg)
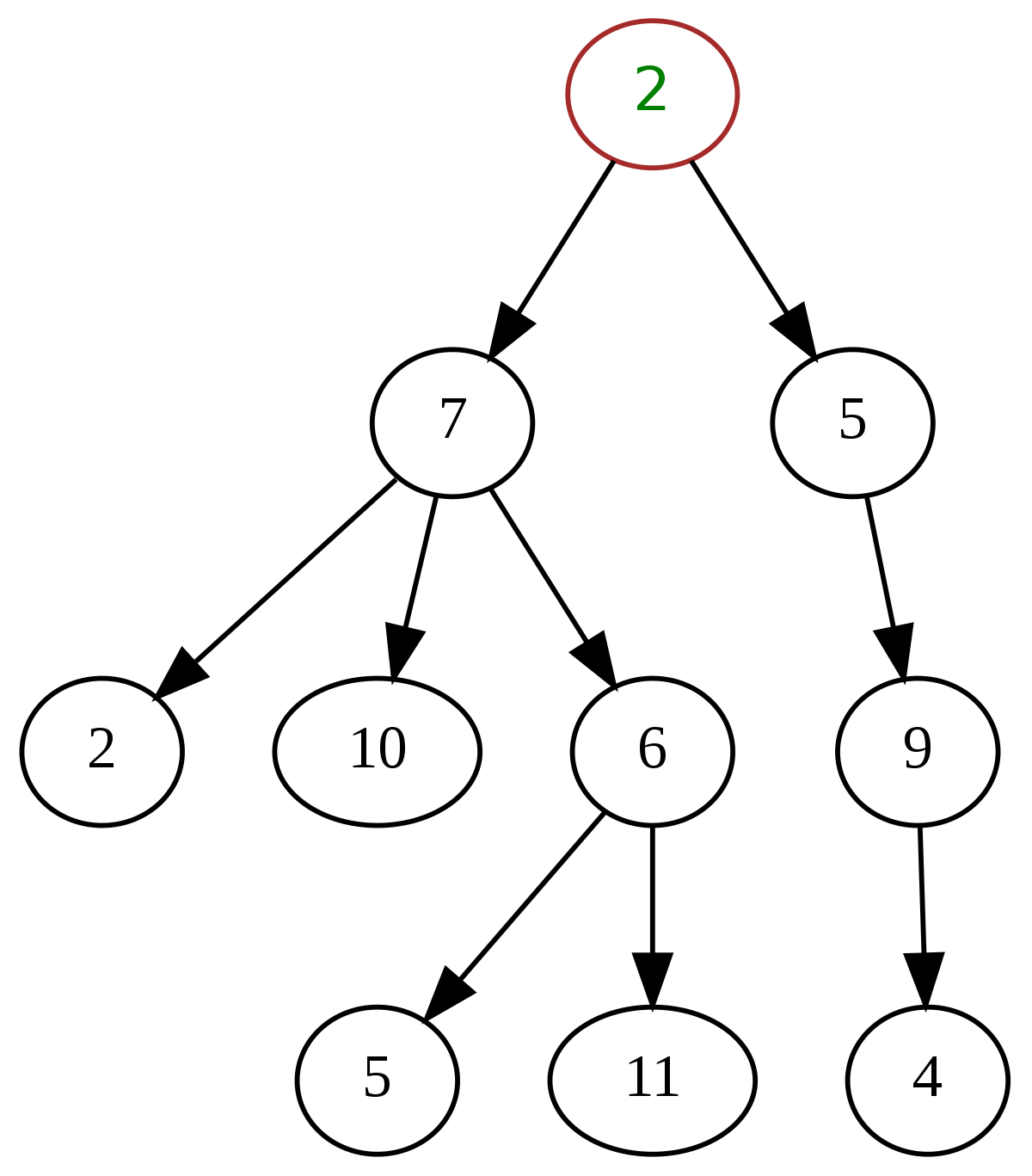
By Paddy3118 - Own work, CC BY-SA 4.0, Link
Un nœud situé à l'extrémité de l'arbre qui n'a donc pas de descendants est une feuille.
Chaque nœud peut avoir un nombre quelconque de nœuds fils, mais il n'a qu'un nœud père (sauf la racine qui n'a pas de nœud père).
- Profondeur d'un nœud
La profondeur d'un nœud est la distance, c’est-à-dire, le nombre d'arêtes de la racine au nœud.
- Hauteur d'un arbre
La hauteur d'un arbre est la plus grande profondeur d'une feuille de l'arbre.
- Taille d'un arbre
La taille d'un arbre est son nombre de nœuds.
Reproduire l'arbre ci-dessus, et l'annoter en légendant:
- la racine,
- des feuilles,
- un nœud père et ses fils.
Calculer la hauteur et la taille de cet arbre.
Arbres binaires
Définition
- Arbre binaire
Les arbres binaires sont un type d'arbres particuliers pour lesquels chaque nœud a au plus deux fils.
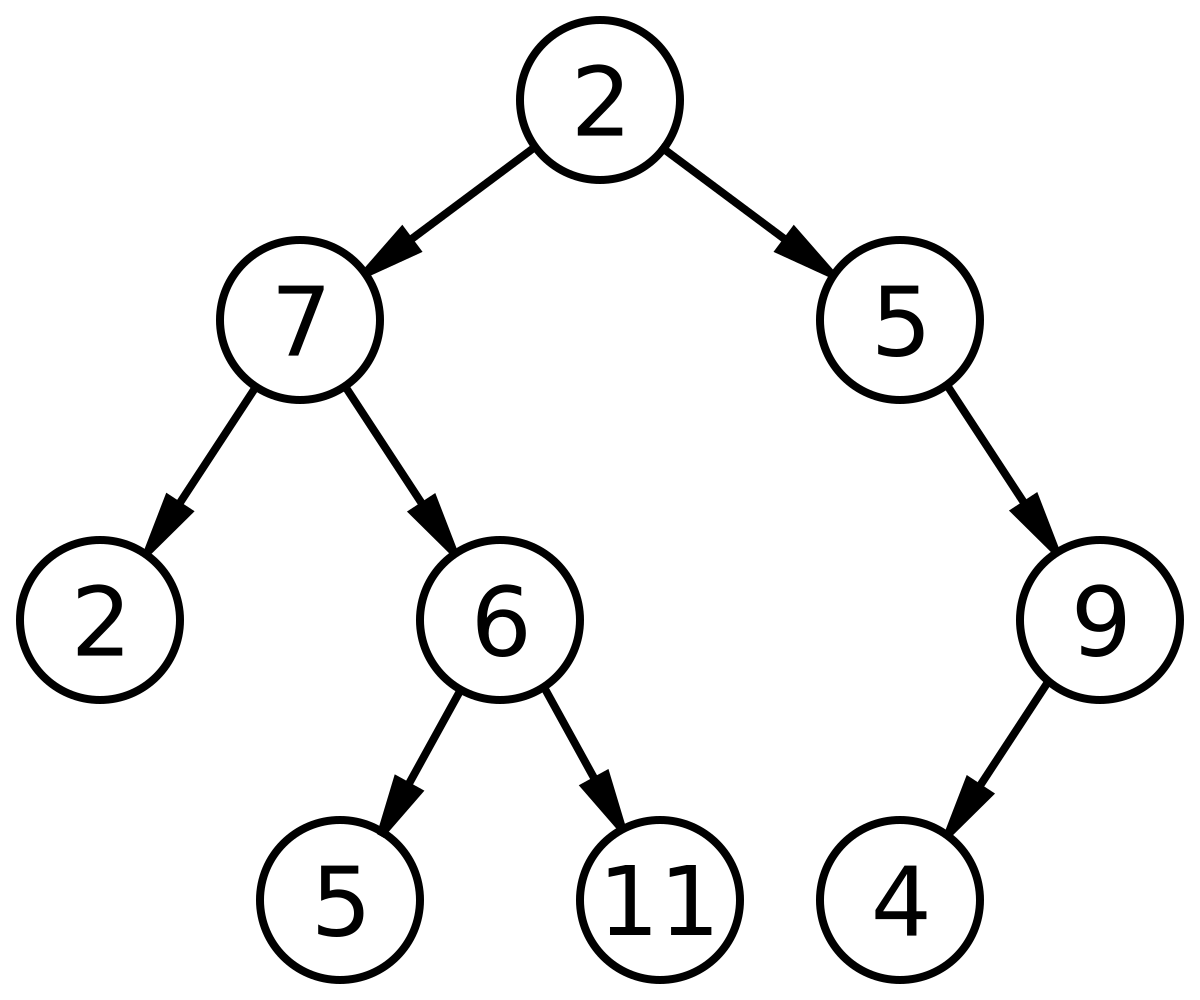
Image par Derrick Coetzee — Travail personnel basé sur : Binary tree.png, Domaine public, Lien
Implémentation récursive
Comme chaque nœud d'un arbre binaire a au plus deux enfants, on définit les sous arbres gauche et sous arbre droit d'un nœud.
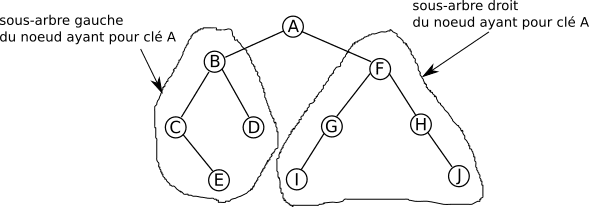CC-BY-SA David Roche
:: prop
Un arbre binaire est une structure de données récursive. Tout nœud d'un arbre binaire est un arbre binaire.
:::
On peut ainsi définir une classe ArbreBinaire récursive comme suit:
class ArbreBinaire:
"""Structure de donnée d'arbre binaire
Attributs
---------
data: type simple int, float, str
étiquette du nœud
gauche: objet de type ArbreBinaire ou None si vide
sous-arbre gauche
droit: objet de type ArbreBinaire ou None si vide
sous-arbre droit
"""
def __init__(self, data, gauche=None, droit=None):
self.data = data
self.gauche = gauche
self.droit = droitÉcrire la séquence d'instructions permettant de construire l'arbre binaire présenté en exemple ci-dessus.
Parcours d'un arbre binaire
Il existe diverses façons de parcourir les nœuds d'un arbre.
Le parcours en largeur d'abord: les nœuds sont parcourus étage par étage, de haut en bas et de gauche à droite.
By Blake Matheny - Transferred from en.wikipedia to Commons., CC BY-SA 3.0, Link
Le parcours en profondeur d'abord: on explore complétement un sous-arbre avant de commencer l'exploration de l'autre. Il existe trois façons de faire:
- Parcours préfixe ou préordre (NGD): on visite d'abord le nœud, puis son sous-arbre gauche, puis son sous-arbre droit.
- Parcours infixe ou en ordre (GND): on visite d'abord le sous-arbre gauche, puis le nœud, puis le sous-arbre droit.
- Parcours postfixe ou en postordre (GDN): on visite d'abord le sous-arbre gauche, puis le sous-arbre droit, et enfin le nœud.
Parcours en profondeur d'abord d'un exemple d'arbre:
- préfixe (rouge): F, B, A, D, C, E, G, I, H;
- infixe (jaune): A, B, C, D, E, F, G, H, I;
- postfixe (vert): A, C, E, D, B, H, I, G, F.
By original images by Pluke, Miles, overlay by User:Jochen Burghardt - File:Sorted binary tree preorder.svg, File:Sorted binary tree inorder.svg, File:Sorted binary tree postorder.svg, Public Domain, Link
Donner les quatre ordres de parcours de l'arbre ci-dessous qui représente une expression arithmétique.
By original image by User:Emergie, modifications by User:Jochen Burghardt - File:AST binary tree arithmetic.svg, numbers replaced by variables, added grey background for nodes, Public Domain, Link
Quel parcours représente la notation habituelle de nos calculatrices actuelles?
Arbres binaires de recherche
Il s'agit d'un arbre binaire dans lequel toutes les valeurs dans le sous-arbre gauche d'un nœud sont inférieures à la valeur à la racine de l'arbre et toutes les valeurs dans le sous-arbre droit d'un nœud sont supérieures ou égales à la valeur à la racine de l'arbre.
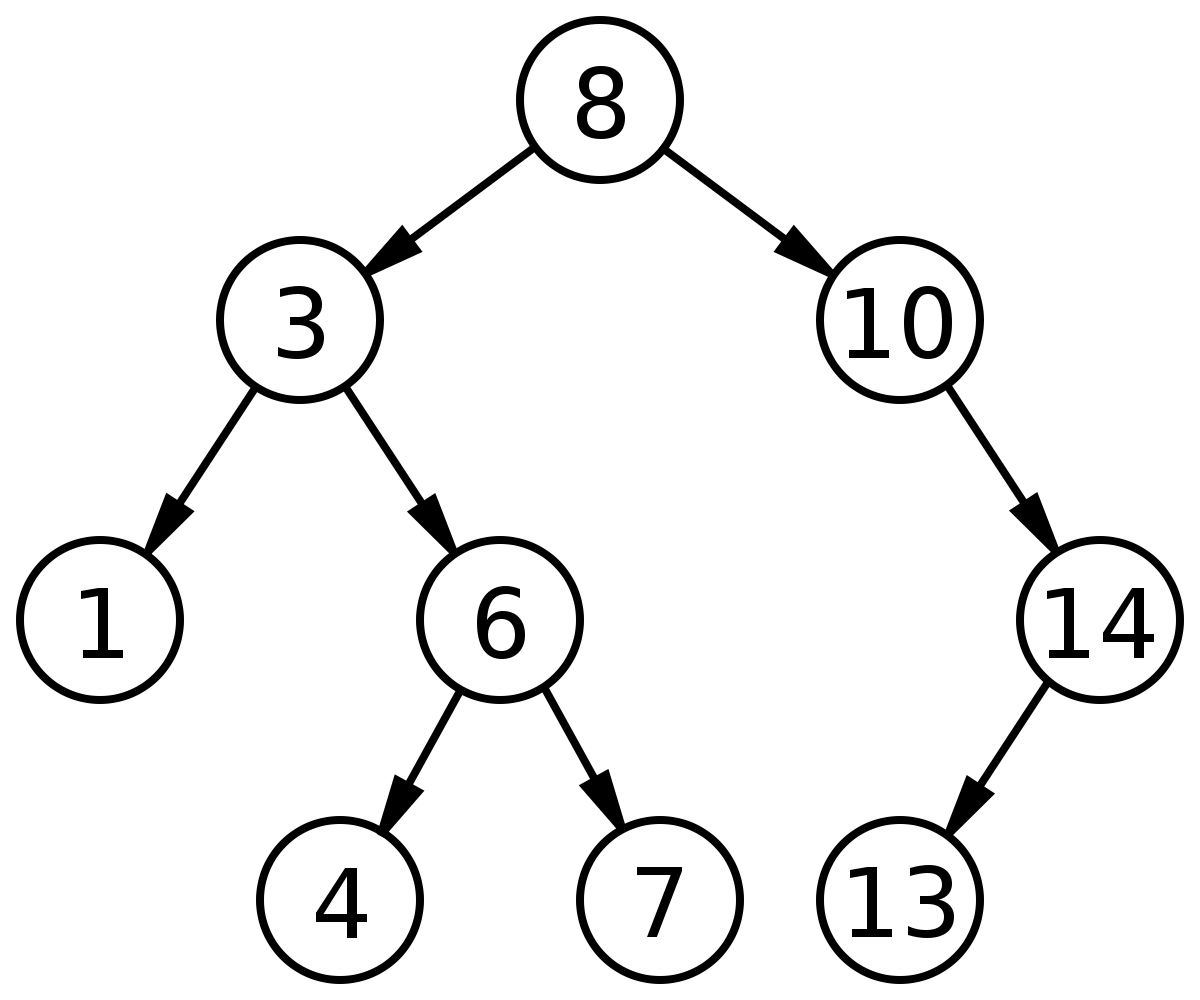Domaine public, Lien
- Proposer deux arbres binaires de recherche avec tous les entiers entre 1 et 6 dont l'un est complet(tous les étages sont entièrement remplis, sauf le dernier ou les feuilles sont tassées à gauche).
- Proposer deux arbres binaires de recherche avec tous les entiers entre 1 et 15 dont l'un est parfait(tous les étages sont entièrement remplis).
Un arbre binaire de recherche permet des opérations rapides pour rechercher une clé, insérer ou supprimer une clé que nous verrons dans la partie algorithmique.
-
Comparer le nombre d'opérations nécessaires à la recherche de l'élément 15 dans l'arbre ci-dessus:
- par une méthode brutale (brute force): on itère sur tous les éléments de l'arbre.
- par une méthode dichotomique utilisant le fait que l'arbre binaire de recherche est « trié ».
- Donner la complexité des deux méthodes pour un arbre de taille .