Programme Officiel
Contenus | Capacités attendues | Commentaires |
|---|---|---|
Algorithmes gloutons | Résoudre un problème grâce à un algorithme glouton. | Exemples : problèmes du sac à dos ou du rendu de monnaie. Les algorithmes gloutons constituent une méthode algorithmique parmi d’autres qui seront vues en terminale. |
Nous allons voir dans ce chapitre comment résoudre des problèmes d'optimisation à l'aide d'algorithmes.
Un problème d'optimisation consiste à minimiser ou maximiser une fonction sur un ensemble.[Wikipedia](https://fr.wikipedia.org/wiki/Optimisation_(math%C3%A9matiques)
L'optimisation d'un trajet sur un GPS, est un problème d'optimisation utilisé quotidiennement qui vise à minimiser le temps de trajet entre deux points A et B sur un réseau routier en respectant le code de la route.
Le problème du sac à dos
Il s'agit d'un problème classique d'introduction aux algorithmes gloutons.
En algorithmique, le problème du sac à dos, noté également KP (en anglais, Knapsack problem) est un problème d'optimisation combinatoire. Il modélise une situation analogue au remplissage d'un sac à dos, ne pouvant supporter plus d'un certain poids, avec tout ou partie d'un ensemble donné d'objets ayant chacun un poids et une valeur. Les objets mis dans le sac à dos doivent maximiser la valeur totale, sans dépasser le poids maximum.
Exploration systématique(force brute)
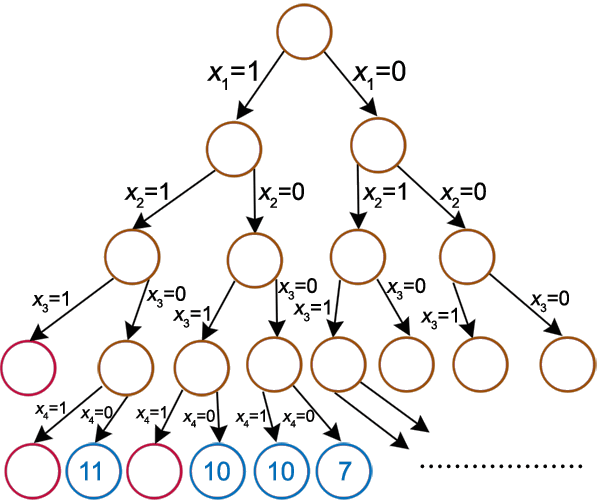
L'exploration de toutes les possibilités consiste à construire un arbre d'exploration binaire.
À chaque fois qu'un objet est ajouté à la liste des objets possibles, la taille de l'arbre est multipliée par 2.
Il s'agit d'une complexité exponentielle ce qui rend cette méthode de résolution inutilisable dans la pratique(Pensez au nombre de routes entre votre maison et le lycée!).
Méthode approximative: l'algorithme glouton
L'algorithme le plus simple est un algorithme glouton. L'idée est d'ajouter en priorité les objets les plus efficaces, jusqu'à saturation du sac :
trier les objets par ordre décroissant d'efficacité
w_conso := 0
pour i de 1 à n
si w[i] + w_conso ≤ W alors
x[i] := 1
w_conso := w_conso + w[i]
sinon
x[i] := 0
fin si
fin pourLes deux phases de l'algorithme glouton.
- À gauche : tri des boîtes par ordre d'intérêt (ici en dollars par kilogramme).
- À droite : insertion dans l'ordre des boîtes, si cela est possible.
On obtient ici une solution de 11$ pour 11 kg alors que la solution optimale est de 12$ et 14 kg.
Le problème du rendu de monnaie
Examinons un autre problème d'optimisation : le problème du rendu de monnaie
Nous sommes des commerçants, nous avons à notre disposition un nombre illimité de pièces de:
- 1 centime
- 2 centimes
- 5 centimes
- 10 centimes
- 20 centimes
- 50 centimes
- 1 €
- 2 €
Nous devons rendre la monnaie à un client à l'aide de ces pièces. La contrainte est d'utiliser le moins de pièces possible.
- Trouvez une méthode gloutonne permettant d'effectuer un rendu de monnaie (en utilisant le moins possible de pièces).
- Vous devez rendre la somme de 2,63 €, appliquez la méthode que vous venez de mettre au point.
- Combien de pièces avez-vous utilisées ?
Sources
- Article Wikipedia
- Site interstices
- cours de NSI sur pixees.fr