Chapitre 10: Mécanique Newtonienne

Étude cinématique

La cinématique est l'étude du mouvement indépendamment des causes qui le provoquent.

Référentiel

Un référentiel est un repère d'espace et de temps par rapport auquel on étudie le mouvement.

Vous avez vu trois référentiels particuliers en classe seconde:

• le référentiel terrestre lié à la surface de la Terre,
• le référentiel géocentrique lié au centre de la Terre mais dont les axes ne tournent pas avec la surface terrestre,
• le référentiel héliocentrique lié au centre du Soleil dont les axes pointent vers des étoiles fixes.

Vecteurs position, vitesse et accélération

Pour décrire le mouvement d'un point matériel M dans un référentiel $\frak{R}$, on utilise 3 vecteurs:

By Maschen - Own work, CC0, Link

Remarque: cette image utilise les notations américaines des vecteurs sans flèche, mais en gras.

• le vecteur position $\vec{r}=\overrightarrow{OM}$ donne les coordonnées en mètre ($m$) du point M:

$\begin{bmatrix} x \\ y \end{bmatrix}$

• le vecteur vitesse $\vec{v}=\frac{d\vec{r}}{dt}$ en mètre par seconde ($m\cdot s^{-1}$) donne les vitesses du point $M$ selon les directions du repère $(O, x, y)$.

$\begin{bmatrix} v_x=\frac{dx}{dt} \\[1.5em] v_y=\frac{dy}{dt} \end{bmatrix}$

• le vecteur accélération $\vec{a}=\frac{d\vec{v}}{dt}$ en mètre par seconde carré ($m\cdot s^{-2}$) donne les variations de vitesses du point $M$ selon les directions du repère $(O, x, y)$.

$\begin{bmatrix} a_x=\frac{dv_x}{dt} \\[1.5em] a_y=\frac{dv_y}{dt} \end{bmatrix}$

Étude dynamique : les lois de Newton

La dynamique s'intéresse au lien entre les mouvements des objets et les forces qu'ils subissent.

Les lois de Newton supposent l'existence de référentiels, que l'on peut supposer immobiles pendant la durée de l'expérience, appelés référentiels galiléens.

2^e loi de Newton : Relation fondamentale de la dynamique

Dans un référentiel galiléen, un système de masse m constante soumis à des forces de somme vectorielle $\sum{\vec{F}}$ subit une accélération $\vec{a}$ inversement proportionnelle à sa masse:

$\sum{\vec{F}}=m \vec{a}$

chute libre sans vitesse initiale

• Établir les équations du mouvement.
• AN: Calculer le temps de chute si z₀= 10 m.

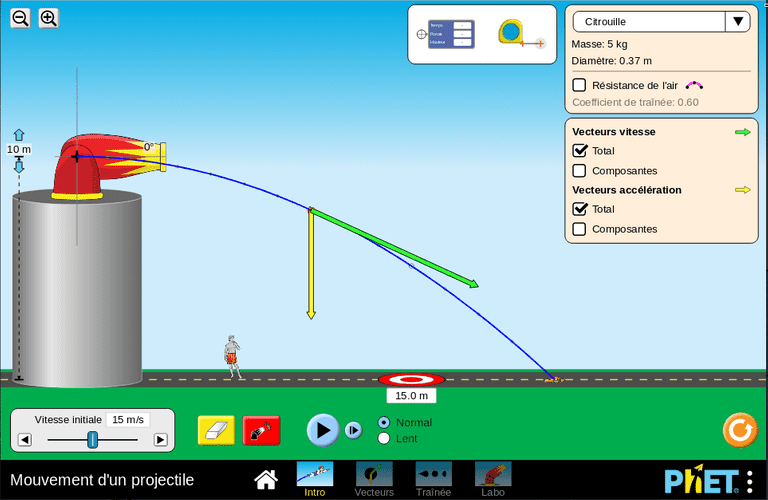
chute libre avec une vitesse initiale horizontale.

• Établir les équations du mouvement.
• AN: Calculer le temps de chute ainsi que la distance parcourue si z₀ =10 m, et v₀= 5m/s.

1^ère loi de Newton : Principe d'inertie

Il ne s'agit qu'un d'un cas particulier de la deuxième loi de Newton lorsque la somme des forces est nulle.

Dans un référentiel galiléen, la vitesse $\vec {v}$ du système est constante, si et seulement si la somme des forces $\Sigma \vec{F}$ s'exerçant sur le corps est nulle.

$\vec {v}=cte \Leftrightarrow \sum {\vec {F}}={\vec {0}}$

3^e loi de Newton : Principe des actions réciproques

A et B étant deux corps en interaction, la force $\vec{\mathrm{F}}_{\mathrm{A/B}}$ (exercée par A sur B) et la force $\vec{\mathrm{F}}_{\mathrm{B/A}}$ (exercée par B sur A) qui décrivent l'interaction sont directement opposées:

$\vec{\mathrm{F}}_{\mathrm{A/B}} = -\vec{\mathrm{F}}_{\mathrm{B/A}}$

Article Wikipedia sur les lois de Newton

Les lois de Kepler (XVII^e)

Les lois de Kepler décrivent les propriétés principales du mouvement des planètes autour du Soleil.

Elles ont été découvertes par Johannes Kepler à partir des observations et mesures de la position des planètes faites par Tycho Brahe, mesures qui étaient très précises pour l'époque.

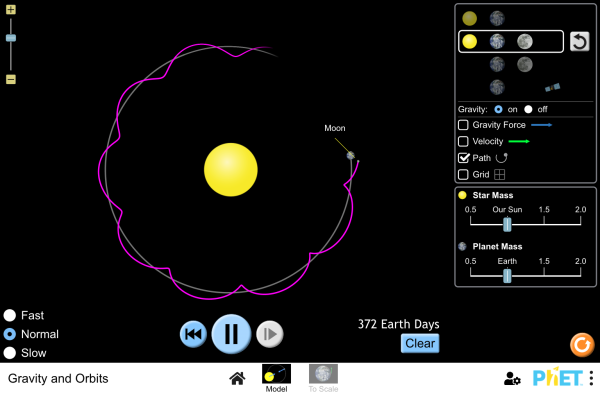
1^ère loi de Kepler ou loi des orbites

Dans le référentiel héliocentrique, la trajectoire du centre d'une planète est une ellipse dont l'un des foyers est le Soleil.

2^e loi de Kepler ou loi des aires

Le rayon planète-Soleil balaie des aires égales pendant des durées égales.

Par Denys (fr) — Travail personnel, CC BY 3.0, Lien

3^e loi de Kepler ou loi des périodes

Le carré de la période de révolution est proportionnel au cube du demi-grand axe de l'orbite.

$\frac{T^{2}}{a^3}=cte$

Vérification numérique

Vérifier la validité de la troisième loi de Kepler pour les planètes du système solaire.

planète	rayon(ua)	T(an)	$\bold{\frac{T^{2}}{a^3}(\frac{an^{2}}{ua^3})}$
Mercure	0,387	0,241
Vénus	0,723	0,616
Terre	1	1	1
Mars	1,52	1,88
Jupiter	5,20	11,9
Saturne	9,55	29,5
Neptune	19,2	84,0
Uranus	30,1	165

Étude des mouvements circulaires

Si une planète a un mouvement circulaire, celui-ci est forcément uniforme d'après la 2^e loi de Kepler.

Accélération

L'accélération est centripète et a pour valeur:

$a=\frac{v^2}{r}$

Vitesse

La vitesse est indépendante de la masse de la planète.

$v=\sqrt{\frac{\mathscr{G}m_S}{R}}$

Démonstration

     

Période de révolution

La période de révolution a pour expression.

$T=2\pi\sqrt{\frac{R^3}{\mathscr{G}m_S}}$

Démonstration

Avant d'exprimer T, on peut démontrer la 3^eloi de Kepler dans le cas des mouvements circulaires.

     

Quantité de mouvement

Définition

Vecteur quantité de mouvement

La quantité de mouvement est le produit de la masse par le vecteur vitesse d'un corps matériel supposé ponctuel.

$\vec{p}=m \vec{v}$

Notations

• $\vec{p}$: quantité de mouvement ($kg \cdot m \cdot s^{-1}$)
• $m$: masse du système ($kg$)
• $\vec{v}$: quantité de mouvement ($m \cdot s^{-1}$)

Forme généralisée de la seconde loi de Newton

Dans le cas général, la deuxième loi de Newton s'écrit :

$\sum{\vec{F}}= \frac{d\vec{p}}{dt}$

Dans le cas particulier ou la masse du système est constante ($\frac{dm}{dt} = 0$), on retrouve:

$\sum{\vec{F}}=m \vec{a}$

Propulsion par réaction

Dans le cas d'un système isolé:

$\sum{\vec{F}}= \frac{d\vec{p}}{dt} = \vec{0} \ soit\ \vec{p} = \vec{cte}$

La voiture lance patate

1. Montrer que si l'on néglige les frottements, les quantités de mouvements de la voiture et de la patate sont égales et opposées.
2. Calculer approximativement la vitesse acquise par le véhicule, en évaluant les masses des objets et la vitesse de lancement de la patate.

Un extrait de gravity en illustration

Cet extrait illustre le principe de propulsion par réaction, d'abord en éjectant la matière de l'extincteur, puis en dernier recours, l'héroïne du film lance l'extincteur pour pouvoir s'accrocher in-extremis au vaisseau.